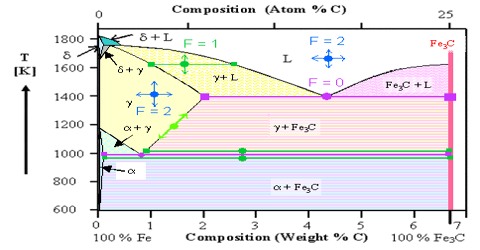
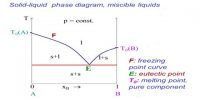
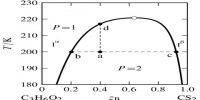
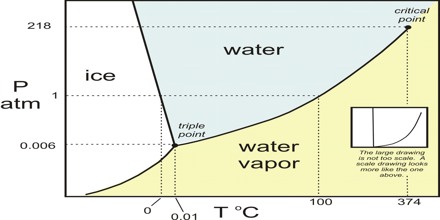
Deduction of the Phase Rule
The relation between the number of phases, number of components and the number of degrees of freedom, as given by Gibbs (1876), is known as the Phase Rule. This rule may be deduced as follows without going through the detailed thermodynamic procedures.
All forms of energy can be resolved into two factors – the intensity factor and capacity factor. For equilibrium purpose only the intensity factor is important. If a substance is present in two different states or phases, equilibrium can only exist if the intensity factor of free energy is the same in both the cases. This intensity factor may be termed as chemical potential and consequently equilibrium can be established if the chemical potential of each component is the same in all phases.
Let there be P phases and C independent components in a system at equilibrium. If a phase consists of C components, its composition can be completely defined by (C – 1) because the concentration of the last component can be obtained by difference. Since there are P phases, P (C – 1) gives the total number of concentration variables of the system. In addition to concentration there are two other variables, e.g., temperature and pressure. Therefore, 2 must be added to P (C – 1), i.e., we obtain P (C – 1) + 2 as the total number of variables. Next we are to consider the number of variables, which are defined by the fact that the phases are in equilibrium, i.e., the number of dependent variable. The number of degrees of freedom is the difference between the total number of variables and the number of dependent variables. Since the chemical potential of a particular component in P phases is the same, for this component the number of dependent variables is (P – 1) as there are (P – 1) equations which determine the equilibrium between the P phases. For C components the number of dependent variables is C (P – 1). Hence, the number of degrees of freedom,
F = P (C – 1) + 2 – C (P – 1) = C – P + 2
This is the well-known phase rule of Gibbs. This is rather a simple rule, but extremely important in discussing equilibria between different phases.
In many systems the vapour phase is not considered and is not included in the discussion. The phase rule for such systems assume the form F = C – P + 1, as 1 is subtracted from the original equation F = C – P + 2, to account for the vapour phase which is not considered. Such systems are said to be condensed systems.