The law of conservation of energy is one of the basic laws of physics and therefore governs the microscopic motion of individual atoms in a chemical reaction. The law of conservation energy states:
“In a closed system, i.e., a system that isolated from its surroundings, the total energy of the system is conserved”.
In SI units, energy has units of Joules. 1 Joule = 1 kg⋅m2⋅s−2
Some forms of energy:
- Kinetic energy – energy of motion.
- Potential energy – energy of “location” with respect to some reference point.
- Chemical energy – energy stored in chemical bonds, which can be released in reactions.
- Electrical energy – energy created by separating charges; energy stored in a battery, for example.
- Thermal energy – energy given off as heat, such as friction.
Since everything has a microscopic origin, the last three are really special cases of potential and kinetic energies, however, the classification is useful.
The kinetic energy of an object of mass m, moving with a velocity v is given by,
KE = ½ mǀvǀ²
Recall that V is the speed v of the particle, so that the kinetic energy can be written as 1/2 mv².
Potential energy is a little less straightforward. Since it is an energy of location with respect to some reference point, the potential energy of an object depends on the specific situation. An example is gravity. An object of mass m at a height h above the Earth’s surface has a gravitational potential energy,
PE = mgh
where g is the acceleration due to the Earth’s gravity. In this example, the potential energy has a simple form, namely that it depends linearly on the height $h$, which describes the object’s location and may even be varying in time if, for example, the object is actually falling toward the Earth.
In general, the potential energy may not be such a simple function of location. In this case, one needs a potential energy curve to describe the potential energy as a function of some coordinate describing the object’s location. Consider the example of a mass attached to a spring moving in one spatial dimension. Let x represent the mass’s position along the x-axis, and let x_0 represent its equilibrium position. As the mass stretches the spring (x>xo), its potential energy increases, and as it compresses the spring compresses (x<xo), its potential energy increases as well. The potential energy can be described by a potential energy function V(x) that is symmetric about $x=xo$, as represented in the figure below:
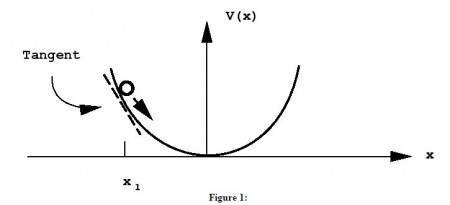
Notice, also, that the mass actually moves under the action of a force, which also changes as a function of x. In fact, the force exerted by the spring on the mass can be determined from the potential energy curve via,
Force at x = – slope of the potential energy curve at x
That is, the force is the slope of the line tangent to the curve at the point $x$, as shown in the figure above for the point x1. In terms of a derivative, the force is given by,
F = – ∂V/∂x
Consider the case of a diatomic molecule:
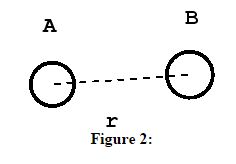
The distance between the atoms A and B is $r$. The chemical forces that hold the molecule together come from a potential energy curve $V(r)$ that depends only on the distance between them. Such a curve might look like:
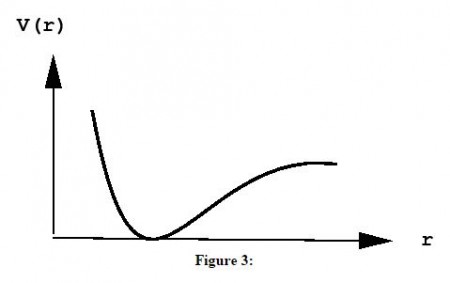
The presence of a deep “well” indicates a particular distance of lowest potential energy. This corresponds to the bond length of the molecule and is, therefore, the most likely value of the separation of the two atoms (think of a ball placed in a gully of this shape – if placed at the bottom of the well, the force on it would be 0, hence it would not move, but would remain there forever unless disturbed).
According to Newton’s second law of motion, force is the action that causes a change in the motion of a particle or sets it in motion from rest. Consider a particle of mass $m$ moving in one dimension so that its position is x. If a force F acts on the particle, it will be set in motion, so that x is no longer a fixed number but a function x(t) of time t. At any instant in time, the particle will have a velocity v defined to be the rate of change of x with respect to time,
v(t) = ∂x/∂t
In general $v$ is not fixed but is also a function v(t) of time t. If v(t) is not constant, in fact, then the particle also has an acceleration a defined as the rate of change of v with respect to time,
a(t) = ∂v/∂t
Since v = ∂x/∂t, it follows that,
a(t) = ∂²x/∂t²
Newton’s second law of motion states that the force F acting on the particle is directly proportion to this acceleration, with the mass $m$ as the constant of proportionality,
F = ma = m(∂v/∂t) = m(∂²x/∂t²)
Since motion generally occurs in three rather than one dimension, position, velocity, acceleration, and force are all vector quantities. The position is usually denoted r, and r has three components r = (x,y,z). Similarly velocity v has components v = (vx,vy,vz), accleration a= (ax,ay,az), and F = (Fx,Fy,Fz). In vector notation,
Newton’s second law reads,
F = ma = m(∂v/∂t) = m(∂²r/∂t²)
Hence, if r is not a fixed vector but a function r(t) of time, this means that each component of r is a function of time r(t) = (x(t),y(t),z(t)).