Law of Rational Indices in Crystal Systems
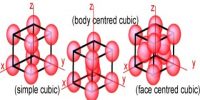
Crystalline solids exhibit different toms depending on the relative sizes of the ions or atoms, type of binding force, nature of stacking, etc. any of the six or sometimes seven main groups into which crystals are commonly classified according to the relative lengths and inclinations of their axes or according to their respective symmetries.
The law of rational indices
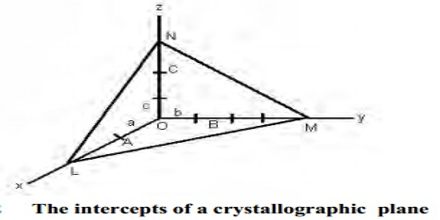
The law of rational indices states that the intercepts of any face of a crystal along the crystallographic axes are either equal to the unit intercepts or some simple whole number multiples of them. The faces of crystals and also planes within crystals can be characterized by means of a suitable set of coordinates. Let consider the three axes OX, OY, OZ (Figure) which are cut by a crystal face ABC at distances OA, OB, and OC from the origin. Let OX, OY, and OZ represent the three crystallographic axes and let ABC be a unit plane. The unit intercepts will then be a, b and c. According to the above law, the intercepts of any face such as KLM, on the same three Axes will be simple whole number multiples of a,b and c respectively. These distances at called intercepts. It is found that if the axes are suitably chosen, the intercepts of different faces upon them bear a simple ratio to each other or a given face may cut an axis at infinity. This is called the law of rational intercepts (or indices).
The law of rational indices was deduced by Haüy (1784, 1801) from the observation of the stacking laws required to build the natural faces of crystals by piling up elementary blocks, for instance, cubes to construct the {110} faces of the rhomb-dodecahedron observed in garnets or the ½{210} faces of the pentagon-dodecahedron observed in pyrite, or rhombohedrons to construct the {21.1} (referred to a hexagonal lattice, {21.0} referred to a rhombohedral lattice) scalenohedron of calcite. This law states that the ratio of intercepts of different faces of a crystal with the three axes is constant and can be expressed by rational numbers that the intercepts of any face of a crystal along the crystallographic axes are either equal to unit intercepts a, b, c or some simple whole number multiples of them.
One century later, i.e. since the discovery of X-ray diffraction by crystals, it was recognized that these three rational indices are directly related to the characteristic directions of the X-ray beam diffracted by samples of the same compound.
Many are familiar with the beautiful shapes of natural and synthetic crystals. The shapes are delimited by planar surfaces. Quartz crystals are nice examples. It turns out that you can always uniquely characterize each face by three positive or negative integers, usually small ones.