Measurement of Surface Tension in Capillary rise method
A number of methods are available for the measurement of surface tension of liquids. Of these a few are described below.
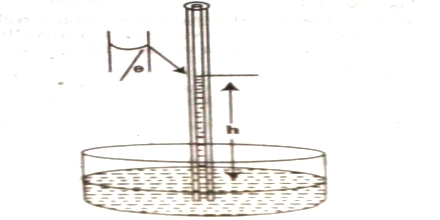
(a) Capillary rise method: This method is the most convenient, simple and gives the most accurate result. The method is based on the fact that when a clean capillary tube which is wetted by the liquid, is dipped in to a liquid the liquid rises in the capillary. The rise of the liquid in the capillary may be understood if it is assumed that a thin film of the liquid adheres to the wall of the capillary. In order to reduce its surface area the liquid rises in the tube. The height to which the liquid column rises is dependent on the surface tension pulling the liquid upward. Equilibrium is reached when the force of surface son is balanced by the force of gravity on the column of liquid. The experimental procedure may be illustratable with reference to Figure.
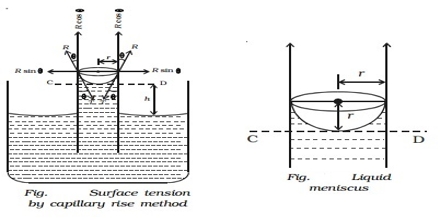
Figure: Measurement of Surface Tension by Capillary rise method
Let r be the radius of the capillary and d be the density of the liquid. At equilibrium let the height of the liquid column above the level in the container be h. The surface of the liquid in the capillary; i.e., the liquid meniscus, makes an angle θ with the wall of the capillary. Consequently the average height (h) of the column is to be taken and is computed as the height of the column up to the bottom of the meniscus plus one-third of the radius of the capillary.
Then the downward force = (h) (area of cross section of the capillary) (d) (g)
= (h) (πr2) (d) (g); where g is the gravitational constant.
As the surface makes an angle θ with the walls and only the vertical component of the force is effective in holding up the liquid column.
The upward force = 2πr γ cosθ
At equilibrium, upward force = downward force;
So, 2πr γ cosθ = h (πr2) dg
or, γ = hdgr/2cosθ
For many liquids, including water, θ is very close to 0 in capillary so that we have;
γ = ½ hdgr … … … (1)
(as cosθ = 1)
Measurement of the quantum on the right hand side of equation (1) gives the value of γ. In order to find the value h a travelling microscope is used and the density of the liquid is measured with a suitable apparatus.