The Poiseuille Equation in Viscosity of Liquids
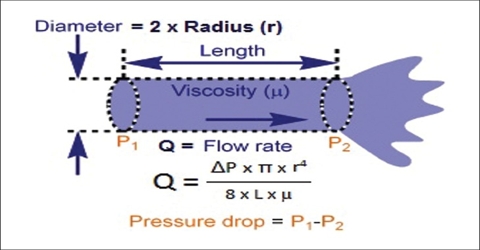
Poiseuille studied the flow of liquids through capillaries and deried an expression for the co-efficient of viscosity. Although the correct version of the formula, which is widely used in measurement of viscosity, was deried Hagenbach the formula is known as Poiseuille equation. Consider a liquid flowing through a tube of length, l, and of circular cross-section with radius, R. The velocity of flow becomes uniform when the pressure drop, P = P1– P2, along the length, l, balances the viscous drag of the liquid. The viscous drag results from the thin film of liquid that adheres to the wall of the tube. This thin film is assumed to be stationary and the rate of flow increases to a maximum at the centre of the tube. If the volume of liquid flowing in t seconds is V, then according to Poiseille;
η = [(π PR4 t) / (8Vl)]

This is Poiseuille equation. This equation has been verified quite accurately for flow of liquids through tubes. The kind of flow consistent with this equation is called laminar or streamlines flow. At high rates of flow or flow in tubes of large diameter the flow type changes to what is known as turbulent flow. In turbulent flow the imaginary layers of liquid do not flow parallel to each other.