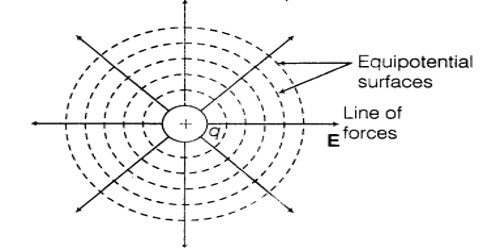
Characteristics and Properties of an equipotential surface
Any surface over which the potential is constant is called an equipotential surface. In other words, the potential difference between any two points on an equipotential surface is zero. It is the surface which is the locus of all points which are at a similar potential is known. No work is mandatory to move a charge from one point to another on this surface.
Characteristics of the equipotential surface:
(i) The surface of a charged conductor is always an equipotential surface. Electric charges on this surface remain stationary.
(ii) Electric lines of force penetrate this surface at the right angle. This can be treated as equipotential volume.
(iii) No work is done in transferring a charge from a point to another point on this surface. No work is required to move a charge.
(iv) Surface or volume of a body can be of the equipotential surface; again surface and volume in space can be of the equipotential surface.
(v) Potential remains the same at all points. The electric field is always normal at every point.
(vi) These are always perpendicular to field lines. It helps us to distinguish the region of the strong field from that of a weak field.
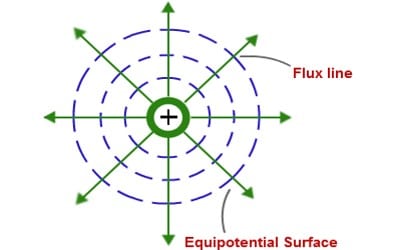
Some important properties of equipotential surfaces:
- Work done in moving a charge over an equipotential surface is zero. They give the direction of the electric field. For a point charge, they are concentric spherical shells.
- Two equipotential surfaces can never intersect. The direction of the surface is from high potential to low potential.
- The electric field is always perpendicular to an equipotential surface. They never cross each other.
- For a uniform electric field, they are planes normal to the x-axis. No work is required to move a charge from the center to the surface.
- In a uniform electric field, any plane normal to the field direction is an equipotential surface.
- The spacing between equipotential surfaces enables us to identify regions of strong and weak fields. They are closer together in the regions of strong fields and farther apart in the region of weak fields
- Two equipotential surfaces can never intersect. If two equipotential surfaces could intersect, then at the point of intersection there would be two values of electric potential which is not possible.
- For an isolated point charge, the surface is a sphere. i.e., concentric spheres around the point charge are different equipotential surfaces.