Coulomb’s law: Mathematical Explanation
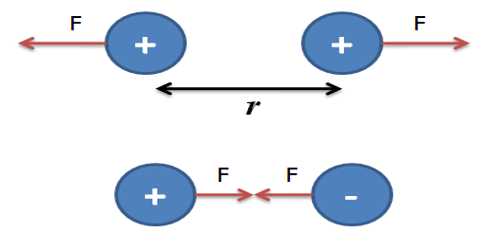
At a particular medium, the magnitude of the attractive or repulsive force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between the charges. The force acts along the straight line joining the two charges.
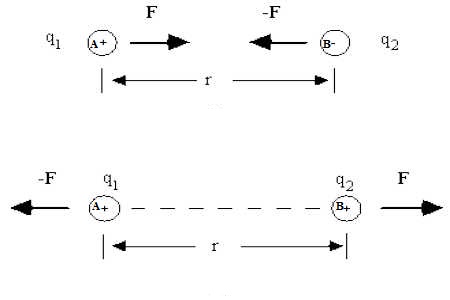
Explanation: let q1 and q2 be two point charges and let r be the distance between them (Fig). If they assert force of magnitude F, then according to Coulomb’s law,
F ∞ q1q2; when ‘r’ is constant.
and, F ∞ 1/r2; where q1 and q2 are constant.
When, r, q1 and q2 all vary, then,
F ∞ q1q2 / r2
or, F = K [q1q2 / r2]
Here, K is proportionality constant. Its value depends on the nature of the medium and the units of F, q1, q2 and r.
In S. I. or M. K. S. unit,
K = 1/4πε, where ε (Epsilon) is the permittivity of the medium in which the charges are located.
F = 1/4πε (q1q2 / r2)
In air or vacuum, the Coulomb law is written as;
F0 = 1/4πε0 (q1q2 / r2) … … … (1)
Here F0 is the force acting in air or in vacuum and ε0 is the permittivity of vacuum.
In S.I. unit, F is expressed in Newton (N), charge in Coulomb (C) and distance in meter (m), so the experimental value of ε0 is
ε0 = 8.854 x 10-12 C2N-1m-2.
and, 1/4πε0 = 1 / [4π x 8.854 x 10-12] = 9 x 109 Nm2C-2.
Hence, from equation (1) We get,
F0 = 9 x 109 (q1q2 / r2) … … … (2)
Unit of charge: In S.I. method the unit of charge is Coulomb.
Definition of 1 Coulomb: We can define 1 Coulomb of charge from equation (2).
If F0 = 9 x 109 N, q1 = q2 = q coul and r = 1 m, then q2 = 1 or, q = ± 1 coul.
i.e., One coulomb is that charge which, when placed at a distance of 1m in a vacuum, from an equal and similar charge repels it with a force of 9 x 109 N.
Nature of force: The value of F can be determined by knowing the values of the quantities of the right-hand side of equation (2). If the determined value of F is positive, then the force will be repulsive, because the product of two similar quantities is positive. On the other hand, if the determined value of F is negative, then the force will be attractive because the product of two similar quantities is negative.