The harmonic oscillations of a physical system results from two basic properties namely elasticity and inertia. Let consider a body displaced from a mean position. The restoring force brings the body to the mean position.
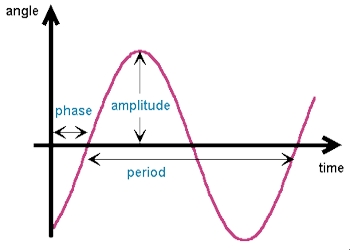
(i) At extreme position when the displacement is maximum, velocity is zero. The acceleration becomes maximum and directed towards the mean position.
(ii) Under the influence of restoring force, the body comes back to the mean position and overshoots because of negative velocity gained at the mean position.
(iii) When the displacement is negative maximum, the velocity becomes zero and the acceleration is maximum in the positive direction. Hence the body moves towards the mean position. Again when the displacement is zero in the mean position velocity becomes positive.
(iv) Due to inertia the body overshoots the mean position once again. This process repeats itself periodically. Hence the system oscillates. The restoring force is directly proportional to the displacement and directed towards the mean position.