A uniform magnetic field exerts no net force on a current loop but it does exert a net torque. Torque (τ) is the twisting force that tends to cause rotation. The axis of rotation is the point where the object rotates.
Torque experienced by a current loop in a uniform magnetic field
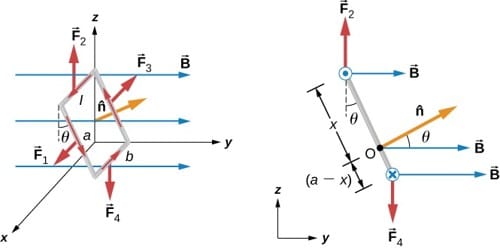
Let consider a rectangular loop PQRS of length l and breadth b (Figure). It carries a current of I along PQRS. The loop is placed in a uniform magnetic field of induction B. Let θ be the angle between the normal to the plane of the loop and the direction of the magnetic field.
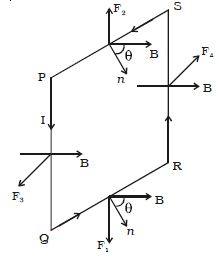
Fig: Torque on a current loop placed in a magnetic field
Force on the arm QR, →F1 = →I(QR) × →B
Since the angle between →I(QR) and →B is (900 – θ),
The magnitude of the force F1 = BIb sin (900 – θ)
F1 = BIb cos θ
Force on the arm SP, →F2 = →I(SP) × →B
Since the angle between →I(SP) and →B is (900 + θ),
The magnitude of the force F2 = BIb cos θ
The forces F1 and F2 are equal in magnitude, opposite in direction and have the same line of action. Hence their resultant effect on the loop is zero.
Force on the arm PQ, →F3 = →I(PQ) × →B
Since the angle between →I(PQ) and →B is 900,
The magnitude of the force F3 = BIl sin 900 = BIl
F3 acts perpendicular to the plane of the paper and outwards.
Force on the arm RS, →F4 = →I(RS) × →B
Since the angle between →I(RS) and →B is 900,
The magnitude of the force F4 = BIl sin 900 = BIl
F4 acts perpendicular to the plane of the paper and inwards.
The forces F3 and F4 are equal in magnitude, opposite in direction and have different lines of action. So, they constitute a couple.
Hence, Torque = BIl × PN = BIl × PS × sin θ (Figure)
= BIl × b sin θ = BIA sin θ
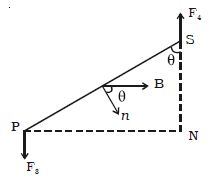
Fig: Torque
If the coil contains n turns, τ = nBIA sin θ
So, the torque is maximum when the coil is parallel to the magnetic field and zero when the coil is perpendicular to the magnetic field.
Torque, τ = F × r
Where, F = force applied and, r = distance between the center of the axis of rotation and to the point where force is applied.
Mathematical Explanation with Example:
Motors are the most common function of the magnetic force on current-carrying wires. Motors contain loops of wire in a magnetic field. When current is passed through the loops, the magnetic field exerts torque on the loops, which rotates a shaft. Electrical energy is converted into mechanical work in the procedure.
[Find the maximum torque on a 100-turn square loop of a wire of 10.0 cm on a side that carries 15.0 A of current in a 2.00-T field.]
Strategy – Torque on the loop can be found using τ = NIABsinθτ = NIAB sinθ. Maximum torque occurs when θ = 90º and sin θ = 1.
Solution
For sin θ = 1, the maximum torque is
τmax=NIABτmax=NIAB
Entering known values yields
τmax = (100)(15.0 A)(0.100 m2)(2.00 T) = 30.0 N⋅mτmax=(100)(15.0 A)(0.100 m2)(2.00 T) = 30.0 N⋅m.