Verification of Conservation Law
Experimental procedure: Exercise the following experiments to verify the conservation principle of momentum.
Experiment- 1: Take two toy cars A and B. Let their masses be m1 = m2 = m. Keeping a compressed spring in the middle tie strongly the two cars by a thread [Fig (a)]. Now burn the thread with a match stick.
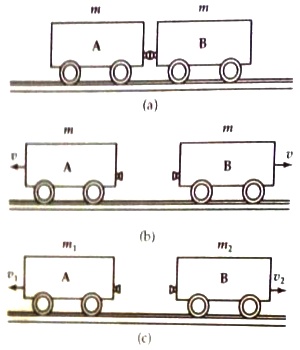
After burning of the thread the spring will expand. So, the two cars will move away from each other in opposite direction and the spring will fall to the ground. Measure the speed of the two cars, you will see that their magnitudes are the same (fig b).
Put two marks on the rail behind two cars by a chalk. A new measure by a stop watch the time for each car to cross the two marks. In this case, divide the distance by time to determine the velocity of the car. This experiment follows the conservation principle of momentum. At first, the two cars were at rest, total momentum was zero. Since the two cars move opposite to each other, so if the velocity of one car is taken as positive then the velocity of the other car will be negative.
So, while in motion total momentum of the two cars = mv – mu = 0 = total initial momentum of the two cars. If the masses of the two cars are m1 and m2 (Fig (c)] and if velocities v1 and v2 are measured as before then it is found that m1v1 and m2v2 are equal. But direction of v1 and v2 are opposite to each other, so total momentum of the two cars is zero.
Experiment- 2: You can do this experiment by taking seven or eight billiard balls of equal mass. Keep all these balls in series touching each other on a smooth table in a straight line (Fig 2). If you strike the series by a rolling ball you will see that a ball from the other end of the series rolls ahead with same velocity.

If you perform the experiment by rolling two halls simultaneously it will be seen that after collision, the two balls from the opposite end of the series roll away with the same velocity. Similarly, if the series is struck by three balls, three balls from the other end of the series will roll away. Naturally, question arises, if two rolling balls strike the series, then why a single ball does not roll away from the other end of the series with double speed? Here, although principle of conservation of momentum is obeyed, but conservation principle of mechanical energy is violated.