English Physicist Robert Hooke (1635 – 1703) in the year 1676 put forward the relationship between the extension produced in a cable and the restoring force developed in it. An ideal spring is remarkable in the logic that it is a method where the generated force is linearly dependent on how far it is stretched; this activity is described by Hooke’s law. The law formulated on the base of this study is known as Hooke’s law.
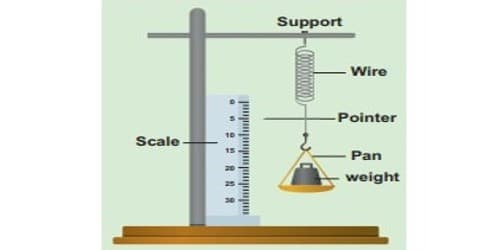
A spring is suspended from rigid support as shown in the Figure. A weight hanger and a light pointer are attached at its lower end such that the pointer can slide over a scale graduated in millimeters.
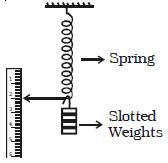
The initial reading on the scale is noted. A slotted weight of m kg is added to the weight hanger and the pointer position is noted. The same procedure is repeated with every additional m kg weight. It will be observed that the extension of the spring is proportional to the weight. This verifies Hooke’s law.
According to Hooke’s law, within the elastic limit, the strain produced in a body is straight proportional to the pressure that produces it. This Law stated above that to extend a spring by an amount dx from its previous position, one needs a force F which is determined by F = kdx. Here k is the spring constant which is a quality of each spring.
(i.e) pressure α strain
Stress / Strain = a constant, known as modulus of elasticity.
Hooke’s Law Formula is given by: F = -kx
Its unit is Nm-2 and its dimensional formula is ML-1T-2.
Experimental verification of Hooke’s law –
Therefore, in order to verify Hooke’s Law, you must prove that the force F and the detachment at which the spring is stretched are comparative to each other and that the constant of proportionality is k.
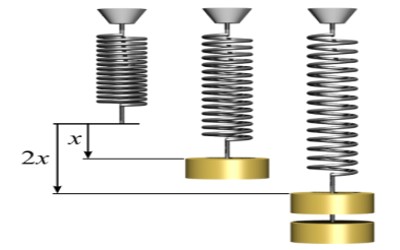
A spring is balanced from a rigid hold as shown in Fig. A weight hook and a light cursor are attached at its inferior end such that the cursor can slide over a scale graduated in millimeters. The primary reading on the scale is noted. A slotted weight of ‘m’ gram/kg is further to the weight hook and the cursor place is noted. It will be experimental that the conservatory of the spring is comparative to the weight. This verifies Hooke’s law.
Method:
- The spring reading meter will measure in its primary face.
- Then the spring placed in the fix of the retort position and hold together strongly adequate to grasp it in position.
Example: A spring is stretched by 5 cm and has a force constant of 2 cm /dyne. Calculate the Force applied?
Given: Force constant k = 2 cm/dyne,
Extension x = 5 cm.
The force applied is given by F = – kx = – 2cm/dyne * 5 cm = – 10 cm/dyne.