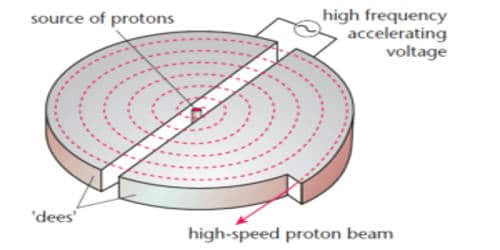
A cyclotron is a device used to accelerate charged particles to high energies. It works on the principle that a charged particle moving normal to a magnetic field experiences magnetic lorentz force due to which the particle moves in a circular path. It was devised by Lawrence.
It consists of a hollow metal cylinder divided into two sections D1 and D2 called Dees, enclosed in an evacuated chamber (Figure). The Dees are kept separated and a source of ions is placed at the center in the gap between the Dees. They are placed between the pole pieces of a strong electromagnet. The magnetic field acts perpendicular to the plane of the Dees. The Dees are connected to a high-frequency oscillator.
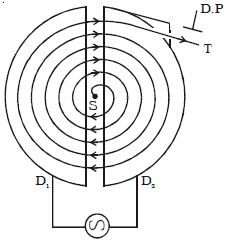
Fig: Construction of Cyclotron
Working:
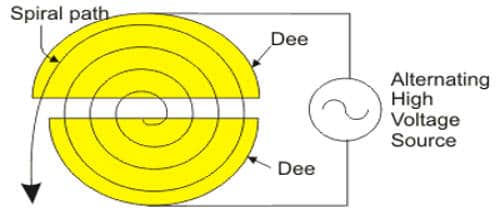
The working of a cyclotron is based on the fact that the frequency of revolution of the charged particles is not dependent on the energy. When a positive ion of charge q and mass m is emitted from the source, it is accelerated towards the Dee having a negative potential at that instant of time. By the time the ion arrives at the gap between the Dees, the polarity of the Dees gets reversed. Hence the particle is once again accelerated and moves into the other Dee with a greater velocity along a circle of greater radius. Thus the particle moves in a spiral path of increasing radius and when it comes near the edge, it is taken out with the help of a deflector plate (D.P). The particle with high energy is now allowed to hit the target T.
When the particle moves along a circle of radius r with a velocity v, the magnetic Lorentz force provides the necessary centripetal force.
Bqv = (vm2 ) / r
v /r = Bq / m = constant …(1)
The time taken to describe a semi-circle
t = π r / v … … … (2)
Substituting equation (1) in (2),
t = π m/ Bq … … … (3)
It is clear from equation (3) that the time taken by the ion to describe a semi-circle is independent of
(i) the radius (r) of the path and (ii) the velocity (v) of the particle
Hence, period of rotation T = 2t
T = 2 π m / Bq = constant …(4)
So, in a uniform magnetic field, the ion traverses all the circles in exactly the same time. The frequency of rotation of the particle,
v = 1 /T = Bq / 2 πm … … … (5)
If the high frequency oscillator is adjusted to produce oscillations of frequency as given in equation (5), resonance occurs.
The cyclotron is used to accelerate protons, deuterons, and α – particles.
Limitations
- Light particles like electrons (e-) and positron (e+) cannot be accelerated by cyclotron as frequency will no more be constant. So resonance conditions cannot always be satisfied.
- Maintaining a uniform magnetic field over a large area of the Dees is difficult. As cyclotrons are very big, it is difficult to maintain a constant magnetic field over a large area.
- At high velocities, a relativistic variation of mass of the particle upsets the resonance condition.
- At high frequencies, a relativistic variation of mass of the electron is appreciable and hence electrons cannot be accelerated by a cyclotron.