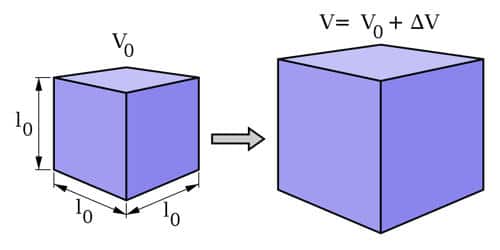
The volume of a solid substance increases if its temperature is increased. It is called volume expansion. Thermal expansion is the tendency of matter to change in volume in response to a change in temperature. The degree of expansion divided by the change in temperature is called the material’s coefficient of thermal expansion; it generally varies with temperature.
Let, the initial volume of a substance be V1 and the initial temperature is θ1. When the temperature is raised to θ2, its volume becomes V2 after being increased.
There increase in volume is V2 – V1 and increase of temperature = θ2 – θ1
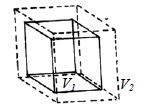
Now if the coefficient of volume expansion is represented by
γ = [(V2 – V1) / V1(θ2 – θ1)] ….. ………. ………(1)
[Increase in surface area / (Initial area x increase of temperature)]
[Note that the volumetric expansion coefficient used in the calculator is constant. If you want to calculate volumetric change for a liquid over a temperature range where the volumetric expansion coefficient for the liquid changes a lot – interpolate the coefficient values, or split the calculation in the different temperature ranges.]
In equation (1) if the initial volume V1 = 1 m3 and increase of temperature, θ2 – θ1 = 1K, then
γ = V2 – V1 = increase in volume.
Therefore, the increase in the volume of a solid of volume 1 m3 for a rise of temperature 1K is called the coefficient of volume expansion of the material of the solid. The coefficient of volume expansion of copper is 50.1 x 10-4 m3 means that if the temperature of a copper body with a volume of 1 m3 increases through 1K then its volume will increase by 50.1 x 10-4 m3.
The relations among α, β, and γ are as follow: γ = 3α and β = 2α
Example – water is a liquid where the volumetric expansion coefficient changes a lot with temperature. Water has its highest density and smallest volume at 40C (39.20F). The volumetric coefficient for water is negative below 40C and indicates that the volume decreases when the temperature moves from 00C (320F) to 40C.