Consider a body of mass M at the point C. Let P be a point at a distance r from C. To calculate the gravitational potential at P consider two points A and B. The point A, where the unit mass is placed is at a distance x from C.
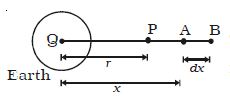
The gravitational field at A is E = GM/x2
The work done in moving the unit mass from A to B through a small distance dx is du = dv = -E.dx
Negative sign indicates that work is done against the gravitational field.
dv = – GM/x2 dx
The work done in moving the unit mass from the point P to infinity is:
∫ dv = – ∞∫r GM/x2 dx
So, v = – GM/r
The gravitational potential is negative, since the work is done against the field. (i.e) the gravitational force is always attractive.