Kirchoff’s voltage law states that the algebraic sum of the products of resistance and current in each part of any closed circuit is equal to the algebraic sum of the emf’s in that closed circuit. This law is a consequence of conservation of energy.
In applying Kirchoff’s laws to electrical networks, the direction of current flow may be assumed either clockwise or anticlockwise. If the assumed direction of current is not the actual direction, then on solving the problems, the current will be found to have negative sign.
If the result is positive, then the assumed direction is the same as actual direction.
It should be noted that, once the particular direction has been assumed, the same should be used throughout the problem. However, in the application of Kirchoff’s second law, we follow that the current in clockwise direction is taken as positive and the current in anticlockwise direction is taken as negative.
Let consider the electric circuit given in Figure
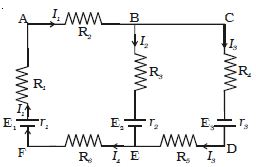
Fig: Kirchoff’s laws
Considering the closed loop ABCDEFA,
I1R2 + I3R4 + I3r3 + I3R5 + I4R6 + I1r1 + I1R1 = E1 + E3
Both cells E1 and E3 send currents in clockwise direction.
For the closed loop ABEFA
I1 R2 + I2R3 + I2 r2 + I4 R6 + I1 r1 + I1 R1 = E1 – E2
Negative sign in E2 indicates that it sends current in the anticlockwise direction.