Relation between Simple Harmonic Motion and Circular Motion
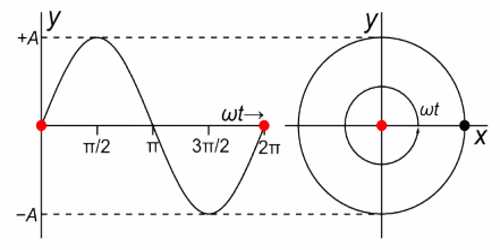
Circular motion is one type of simple harmonic motion. That means, circular motion obeys characteristics of simple harmonic motion. Now observe the figure for establishing a relation between simple harmonic motion and circular motion.
Let a particle start from A and move at angular velocity ω round a circular path ABCD in anti-clockwise direction [Fig. a]. Let O be the centre of the circle and A be its radius. Let after time t the particle reach the position P. Now from point P draw a normal PN on diameter BOD. Then N will be end point of the normal.
Let ON = y, so from triangle OPN we get,
y = OP sin θ = A sin θ
As the particle revolves at uniform angular velocity, so
∠POA = θ = ωt
angle θ is called phase angle or simply phase.
Now, y = A sin θ = A sin ωt
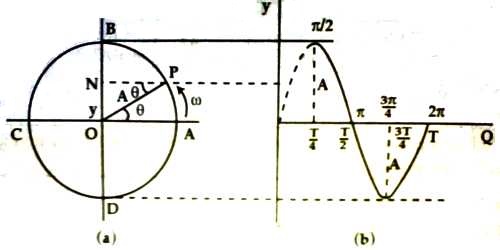
As the particle P mover along the circular path, the end point N on the diameter BOD oscillates along the diameter BOD.
So, velocity of the particle,
v = dy/dt = d/dt (A sin ωt) = A ω cos ωt
and Acceleration,
a = dv/dt = d2y/dt2
= – A ω2 sin ωt = – ω2y … … … (1)
That means, the acceleration of the particle is proportional to its displacement. So, the motion of N is simple harmonic motion. O is the mean position or equilibrium position of this simple harmonic motion, B and D are the end positions and P is the generating point. The circle is called reference circle and the particle is called reference particle. It is to be noticed that while the particle completes one round along the path ABCDA, then the end point N starting from initial position completes the motion along the diameter OBODO and comes back to the initial position. Now the time taken to complete one oscillation is called its time period, T. At that time the end point also completes one round about displacement.
So, T ∞ 2π/ω [θ = ωt and when θ = 2π, t = T, so, 2π = ωT]
In equation (1), some values of θ or ωt are inserted and corresponding displacement are found out. These values are shown in table. The time period of the particle is T. Now if the times for arriving at points B, C, D and A are expressed in T, then they will be respectively, T/4, T/2, 3T/4 and T.
Table:
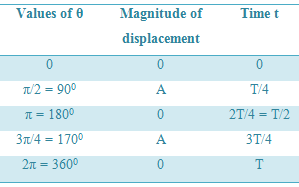
When the particle P resolves at uniform angular velocity, then change of end point N, which represents displacement of particle, is shown in figure b.