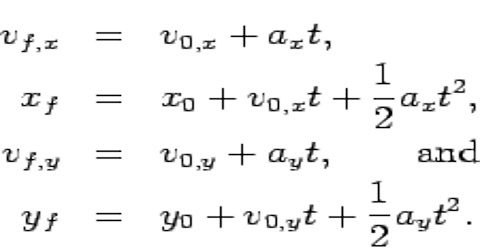Second Equation of Dimensional Motion
In one dimensional motion a body moves along a straight line. So quantities associated with motion, for example displacement, velocity, acceleration etc., have only one component (moving along X-axis will have X-component and Y and Z components will be zero). In deriving equations of linear motion we will consider that the body is moving along X-axis. In that case subscripts associated with different quantifies of motion may be omitted. Normally, vx will be represented by v and ax by a.
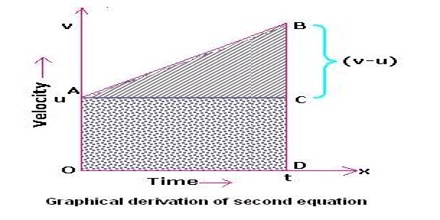
Second Equation:
Equation of motion relating final velocity, acceleration and time (v = v0 + at or vx = vx0 + axt)
Derivation: Let an object’s velocity at time, t = 0 be represented by v0 and at a later time t, its velocity is v.
Now the change of velocity is v – v0 during a time t – 0; its average acceleration during that time is
a = (v – v0)/( t – 0)
Since the object is moving with uniform acceleration, so “a” is equal to the instantaneous acceleration “a”.
so, a = (v – v0)/ t
or, (v – v0) = at
or, v = v0 + at … … … (1)
If initial velocity of the object is zero; i.e., the object starts from rest, then v0 = 0. So equation (1) become
v = at
For one dimensional motion, say along X-axis, let, v0 = vx0; v = vx and a = ax; then we get from equation (1):
vx = vx0 + axt
Similarly, for motion along Y and Z-axis equation (1) reduces to,
vy = vy0 + ayt
vz = vz0 + azt
Instead of uniform acceleration if the objects moves with uniform retardation, then “-a” should be inserted in the above equation.