Simple Harmonic Force is Opposite and Proportional to Displacement
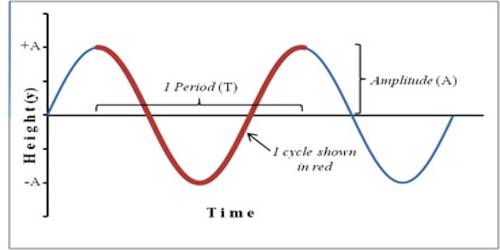
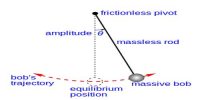
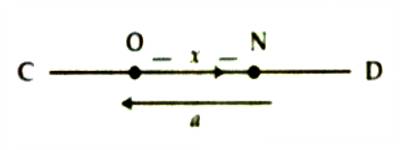
Harmonic motion is a special type of vibrational motion. Suppose, an oscillating particle N between points C and D will indicate a straight line [Figure]. O is the point of equilibrium of the particle and at any time displacement at the particle from equilibrium position is x. If the motion of the particle is harmonic, then the acceleration of the particle at that moment is proportional to x and its direction is along O, i.e., displacement a is opposite to the direction of x. So we can write-
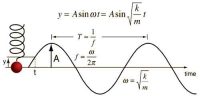
a ∞ – x or, a = – kx
here, k = constant = mω2, m is the mass of the particle and ω is the angular velocity of the particle.
So, a = – mω2x … … … (1)
Again, we know how acceleration varies with time. According to Newton’s second law, when a force acts on a body acceleration is created. That mean,
F = ma
So, F = – mω2x (according to equation 1)
or, F = – (mω2) x or, F = – kx
So, F ∞x
That means, simple harmonic force or restoring force is opposite and proportional to displacement.