Example 1: An object goes around a vertical circular track, as shown. Find the minimum speed of the object near the top of the loop, so that it does not loose contact with the track.
Solution: We draw the free-body diagram of the object when it is near the top. We have the weight mg (down) and the normal force FN (down).
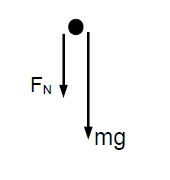
Newton’s second law then gives,
FN + mg = m (v2 /r)
The object barely completes the loop when it is ‘weightless’ near the top: FN = 0. We thus find a condition for the smallest speed:
mg = m (v2min/r), → vmin= √(gr)
For r = 15.0 m, we find vmin = √(9.8 m/s2 • 15.0 m) = 12.1 m/s.
Example 2: Calculate the length of a (sidereal) month from the distance between the Earth and the Moon REM = 3.85 x 108 m.
Solution: We find the mass of the Earth and the Moon from tables ME = 5.98 x 1024 kg and MM = 7.35 x 1022 kg. We thus have ME >> MM, and assume that the Moon rotates about the center of the Earth:
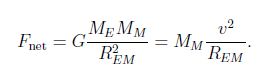
The orbit of the Moon is (nearly) circular, so that for the speed v = 2πREM / T, where T is the period [i.e., the length of a month], we find,
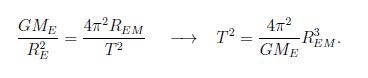
We condude that the square of the period is proportional to the third power of the radius of the orbit this is essentially Kepler’s third law of planetery orbits, for the special case when the orbit is a circle. We find the numerical value,
T = √ (4π2 (3.85 x 108 m)3 / (6.67 x 10-11 Nm2 * 5.98 x 1024 kg)
= 2.28 x 106 s
or 27.5 days (the value in tables is 27.3 days — the difference is due to simplifications made in our calculation).