A special case of interference applies when a wave interferes with a reflected wave: the two waves are automatically vibrating in phase. We consider the case when the original wave travels to the right [Frame I]. The reflected wave is generated at the wall and travels to the left. The superposition of the original and the relected yields the pattern shown in Frame 2. This pattern changes with time [transient behavior]. After a long time, t = ∞, the pattern of crests and troughs is time-independent [stationary]. There are locations, where the (vertical) displacement is always zero; these locations are called nodes. In the middle between two nodes is a location with maxium (vertical) displace- ment. The locations of maximum displace- ments are referred to as antinodes [Frame 3]. Each part of the string moves in `unison;’ that is, each anti no de reaches the maxium displacement at the same time, while at other times, the displacements are less than the maximum value [Frame 4].
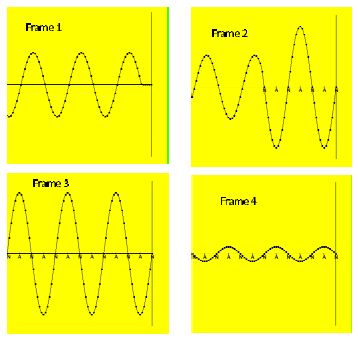
This resulting wave is referred to as a standing wave and is independent of the nature of the wave [transverse or longitudinal] and thus applies to a wave along a string [as shown], the sound waves in an organ pipe, etc.
The time between successive maximum displacements is the period, or the inverse of the frequency of the wave, T =1/f. The distance between neighbouring nodes is half a wavelength λ/2. If the two ends of a rope are fixed, or the two ends of a pipe are closed, the wave has nodes at the two ends so that L = nλ/2, for some integer n. = 1, 2, 3, …. This implies that the length of the rope or the organ pipe determines the frequencies of the produced sound:
fn = v/λn = (v/2L) n, n = 1,2,3… …..
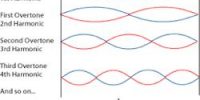
The different cases are called the I/ -th harmonics, i.e., first, second, etc harmonic. In a music context, the second (third) harmonic is called the first (second) overtone.
If one end is fixed and the other end swings freely [e.g., one end of the organ pipe is open, while the other side is closed] then there is a node at the fixed end and an antinode at the open end. We get for the length L = nλ/4 for n = 1, 3, 5, … so that for the possible frequencies,
fn = n (v/4L), n = 1,3, 5, …
That is, there are no even harmonics in ‘asymmetric’ situations.