We consider a rope [elastic string] and excite it by attaching a vibrator at one end. A transverse wave develops along the wave that is travelling along the x-axis. Each (small) element of the string can be considered to be a harmonic oscillator along the vertical The elasticity of the rope provides a coupling between oscillators: if a particular oscillator moves up (down), the oscillators in its vicinity also move up (down).
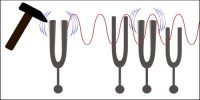
The oscillator at the end with the vibrator undergoes driven harmonic motion. As a result, the amplitude A of the oscillator is much larger than the maximum displacement of the vibrator. We can find an expression for the wave speed using dimensional analysis. We replace the wavelength by the length of the rope λ ≈ L. We assume that the elastic coupling between the neighbouring pieces of the rope produces an “effective” spring constant k. If the mass of the spring is m, then the period of the oscillatory motion is T ≈ √ (m/k).
The wave speed follows v ≈ L √ (k/m) = √kL(m/L). The quantity m/L is the mass per unit length, and we identify kL with the tension along the string T ≈ kL. Despite the approximate nature of our calculation, we arrive at the correct expression for the wave speed:
v = √ ((T/ (m/L))
If the rope is pulled more ‘taut, i.e. when the tension is increased, the wave speed increases.
For sound waves in a gas [longitudinal waves], we consider a volume element V = L3. We write the force in terms of the pressure F = PL2, v ≈ √ PL2 (m/L) = √ (P/ (L/m3)). The expression in the denominator is the density so that v = √(P/p). In the next chapter, we see that the density of a gas is proportional to the pressure and inversely proportional to the (absolute) temperature T, p = m/V = MP/kT, where is the mass of a molecule and k [k = 1.38 x 10-21 J/K ] is the Boltzmann constant, v ≈ √ (kT/M). This yields:
v= √ (λkT / M)
where the adiabatic exponent λ = 5/3 for diatomic gas, such as air. For most applications, the sound speed can be assumed constant v = 345 m/s. The sound speed depends on the phase of the material [solid, liquid, or gas],
Vgas < Vliquid < Vsolid
Typical values are v ≈ 5000 m/s for sound in solids, v ≈ 1000 m/s for liquids, and v ≈ 500 m/s for gases.
Example: A guitar string has length L = 0.56 m and mass m = 2.4 g. Find the tension of a guitar string so that the speed of the transverse wave is equal to the speed of sound in air.
Solution: We solve for the tension along the string:
F = (m/L) v2 = (2.4 x 10-3 kg / 0.56 m) (345 m/s)2 = 510 N.
Discussion: When a musician “tunes” the guitar, the wave speed along the string changes. Because the wavelength is fixed, the frequency of the sound changes as a result of the change in the wave speed.