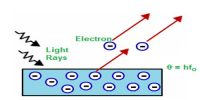
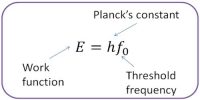
Consider a metallic sphere of radius ‘a’ and density p to fall under gravity in a liquid of density. The viscous force F acting on the metallic sphere increases as its velocity increases. A stage is reached when the weight W of the sphere becomes equal to the sum of the upward viscous force F and the upward thrust U due to buoyancy (Figure). Now, there is no net force acting on the sphere and it moves down with a constant velocity v called terminal velocity.
W – F – U = O … (1)
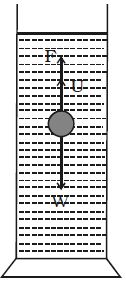
Terminal velocity of a body is defined as the constant velocity acquired by a body while falling through a viscous liquid.
From (1), W = F + U … (2)
According to Stoke’s law, the viscous force F is given by F = 6πη av
The buoyant force U = Weight of liquid displaced by the sphere = 4/3 πa3 σg
The weight of the sphere, W = 4/3 πa3 ρg
Substituting in equation (2),
4/3 πa3 ρg = 6πη av + 4/3 πa3 σg
So, V = 2/9 [a2 (ρ-σ)g]/η