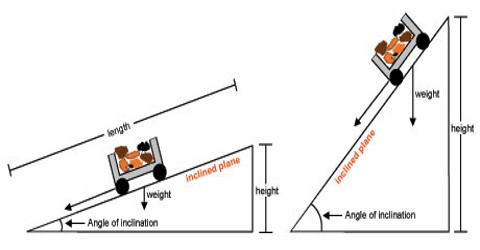
Work done in bringing down through an inclined plane:
Let a body of mass ‘m’ move from point A to B through a polished inclined plane. If g is C acceleration due to gravity, then force of gravity will pull the body directly downward [Figure).
Suppose the angle between displacement and the direction of the force of gravity is θ and AB = s.
Component of displacement along the force of gravity, mg = s cos θ.
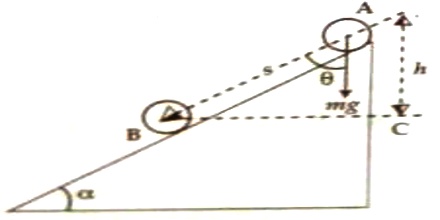
If there were no inclination, the time at which the body moves from A to B. It would have come down by AC = h distance.
h = cos θ
Work, W = mgs cos θ or, W = mgh
If the surface remains at an angle α with the horizontal, then θ = (900 – α)
W = mgs cos (900 – α) = mgs sin α
It is seen from work done by elastic force and force of gravity that,
Work done by elastic force, W = ½ Kx2; W = (displacement)2
On the other hand, work done by the force of gravity,
W = mgh; Work, W ∞ displacement.
So, it can be said that work done by elastic force is directly proportional to the square of displacement. On the other hand work done by force of gravity is directly proportional to displacement or height. If the magnitude of acceleration due to gravity is increased work done by this force also increases.
Work done in case of raising a body:
If a body of ‘m’ is raised at height ‘h’ against the force of gravity, then,
Work = mass x acceleration due to gravity x height
or, W = mgh
This work is, of course, negative.