Question 1:
The concentration of the reactant in a first-order chemical reaction decreases with time as it is consumed to form products and the concentration of [A] varies with time as follows
[A] = [A]0 e-kr
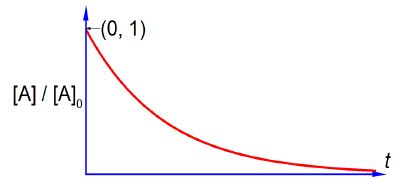
Where [A]0 is the initial concentration of the reactant at time t = 0, [A] is the concentration of the reactant at time t, and k is the rate constant for this particular reaction. Sketch the shape of the graph of [A]/[A]0 plotted as the y-axis against time t plotted as the x-axis and label the two axes. You do not need to calculate anything. Below Figure shows the shape of a negative exponential curve.
Question 2:
[A] = [A]0 e-kt
Write the natural-log form for a kinetic first-order reaction with ([A]/[A]0) as the subject.
Solution 1:
[A]= [A]0 e-kt or, [A]/ [A]0 = e-kt
Remember that k is a constant for a given reaction at a fixed temperature and plotting [A]/[A]0 versus t is a negative exponential and has the shape sketched in below Figure which has an intercept at [A]/[A]0 = 1 that is [A] = [A]0 at t = 0. Note that using this non-linear plot it is not easy to deduce the rate constant k.
Solution 2:
[A]= [A]0 e-kt
From the first order kinetics equation: (1) take natural logs throughout; (2) expand out the right hand side which is the log of a product of two terms into the sum of the log of each term;
ln [A]= ln {[A]0 e-kt }
ln [A]= {ln [A]0} {ln e-kt }
(3) the natural log of the exponential is just the exponent -kt (4) move ln([A]0) to the left hand side by subtracting ln([A]0) from both sides; (5) convert the difference of two logs into the log of the ratio.
ln [A] = ln [A]0 – kt
ln [A] – ln [A]0 = – kt
ln {[A]/[A]0} = – kt