Radioactive decay is a first-order chemical reaction which follows an exponential decay in the reactant, the radioactive element. Starting with an original number of radioactive atoms n0 at time zero, the number of radioactive atoms left, n, after a certain time t is given by
n = n0 e-kt
Where k is the rate constant for this decay reaction. The decay of 238U has a rate constant of k = 1.54 x 10-10 year-1 for the reaction
238U → α + 234Th
Where α is an alpha particle, a fast moving helium 4He2+ nucleus. Calculate the fraction of the uranium decayed after 4.51×109 years, roughly the age of the Earth.
Using the “exp” nomenclature for clarity
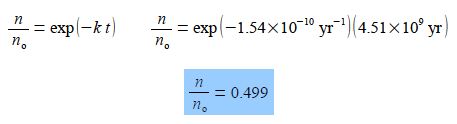
Thus during the lifetime of the Earth about half of the 238U originally present has been converted to thorium-234 234Th which is itself unstable to fission reactions and decays further.