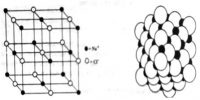
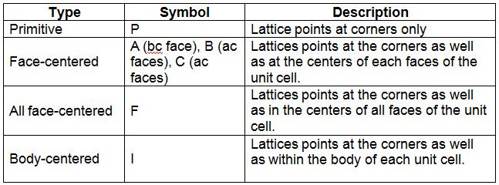
Bravais lattices
A lattice is a regular array of points. Each point must have the same number of neighbors as every other point and the neighbors must always be found at the same distances and directions. All points are in the same environment. In 1850, August Bravais, a French mathematician, studied the detailed internal structure of crystals and came to the conclusion that the lattice points may be present not only at the corners of unit cells, but at the centers of faces or within the body of the unit cells. The description of these lattices are given below:
Brief description of different crystal systems:
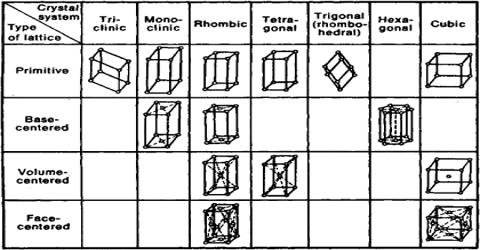
Bravais identified different types of lattices corresponding to seven crystallographic systems. There are 14 ways in which this can be accomplished. These 14 types of lattices are called Bravais lattices. The fourteen Bravais lattices are shown in Table:
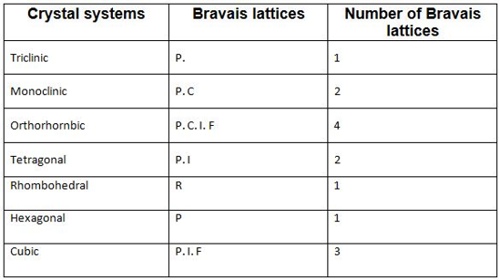
Fig: fourteen Bravais lattices
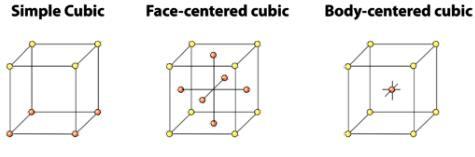
The cubic crystal system has three possible cubic unit cells (a) the simple (also known as primitive) cube, (b) the body-centered cubic and (c) the face-centered cubic. These are illustrated in Figure.