Equation of gravitational constant and acceleration due to gravity
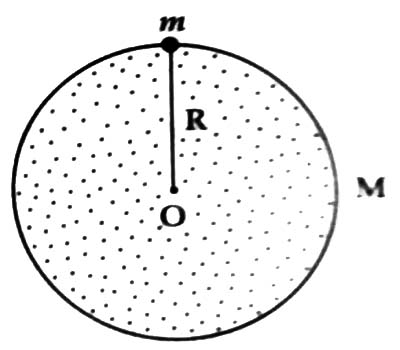
Suppose, a body of mass m is on the surface of the earth and the earth is a round body [Figure]. If the mass and radius of the earth are respectively M and R., then from Newton’s law of gravitation we get.
F = G (Mm/R2) … … … (1)
Again, from Newton’s second law of motion, we get,
F = mg … … … (2)
From equations (1) and (2), we get,
mg = GMm/R2
or, g = G M/R2
This is the expression of g on the surface of the earth.
This is the relation between gravitational constant and acceleration due to gravity. The formula for the acceleration due to gravity is based on Newton’s Second Law of Motion and Newton’s Law of Universal Gravitation.
That means,
acceleration due to gravity = (gravitational constant x mass of the earth) / (radius of the earth)2
According to this equation acceleration due to gravity does not depend on the mass of the body. Again, we know G and M are constant, so the value of g, at a place depends on the distance from the center of the earth to that place. From this, we can come to this conclusion that the value of g at any place on the earth is constant, but it varies with Location.
Consider the mass of the earth, M = 5.983 x 1024 kg and radius of the earth, R = 6.36 x 106 m, then according to the above equation the value of ‘g’ is,
g = [6.657 x 10-11 N-m2.kg-2 x 5.983 x 1024 kg] / [6.36 x 106 m]2 = – 9.846 ms-2
From the relation of gravitational constant and acceleration due to gravity, we can learn the following things –
(i) G is a universal constant, whereas g is a variable constant
(ii) Value of G as 6.657 x 10-11 Nm2kg-2, whereas the value of g is 9.8 ms-2
(iii) G is a scalar quantity, whereas g is a vector quantity
(iv) Value of G does not depend on the mass of the body, nor on the distance of the body from the center of the earth. On the other hand value of g does not depend on the mass of the body, but depends on the distance of the body from the center at the earth.
From the relation of G and g, it would be questioned: Why the earth creates the same acceleration due to gravity to all bodies independent of the mass of the bodies? In answer will say that if M and R are considered respectively the mass and radius of the earth then for a body of mass m on the surface of the earth, we can write,
mg = G mM/R2
where g is the acceleration due to gravity, G is the universal gravitational constant, M is mass, and R is distance. g = GM/R2, since m is absent in the expression, hence acceleration due to gravity is independent of the mass of the body. So, if R is constant, acceleration due to gravity at Place is constant and independent of the mass of the body. Also, when the object is on or near to the surface the value of g becomes constant and does not change considerably with the height.
Again, why G is a universal constant? Since the gravitational force between two parties does not depend on the presence of the medium, nor on the nature of the medium. This force is not dependent on nature, chemical composition or temperature of particles. For these reasons, G is called the universal constant. The acceleration due to gravity is the acceleration produced in the freely falling body due to the influence of the gravitational pull of the earth. However, at large distances from the Earth, or around other planets or moons, the acceleration is different.