Variation due to the rotation of the earth about its axis:
Since the earth is continuously rotating about its own axis, except the bodies present in two poles, all other bodies on earth are moving along a circular path. The centers of these circular paths are on the axis of the earth. For this reason, all the bodies on the surface of the earth experience centrifugal force. Magnitude of the force on the bodies at the equator is maximum and is zero at the two poles. Since the centrifugal force acts opposite to the gravitational force hence a part of gravitational force is spent to balance the centrifugal force, so the weight of the body apparently decreases.
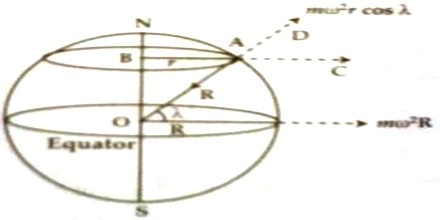
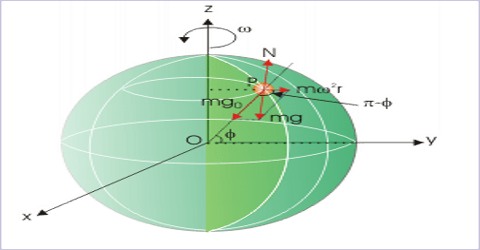
Suppose a body of mass or is located at point A on the surface of the earth at the lattice γ [Figure]. The earth is rotating with angular velocity about its axis NS, so that body rotates with angular velocity ω along the circular path of radius AB = r. If the radius of the earth is R, then r = R cos γ. Due to this rotation centrifugal force mω2r acts on the body along AC. Due to gravitation force F = mg acts on the body along the centre of the earth i.e., along the direction AO. Centrifugal force acting on the body along D i.e., component of opposite to the gravitation is mω2r cos γ. So, apparent weight of the body at point A in will be,
mg – mω2r cos γ = mg – mω2R cos γ;
If the magnitude of acceleration due to gravity at point A is g/ then the apparent weight of the body is mg/.
So, g/ = g [1 – (ω2R cos2 γ /g)]
at the equator, γ = 00; so cos γ = 1
then, g/ = g (1 – ω2R/g) = g – ω2R
Again, at the poles γ = 900; so, cos γ = 0
then, g/ = g
So, value of g changes due to the rotation of the earth about its axis. The value of g becomes minimum at the equator and maximum at the poles. At other places the value of g is in between these two terminal values. It is apparent that the change of the value of g is identical due to the shape and rotation of the earth.