Explain Displacement Current

We can use Gauss’ law to replace p = Ɛ₀ Δ • E in the continuity equation to get

Δ. J + [ϐ (Ɛ₀ Δ • E) / ϐt] = 0

So, Δ . (J + J_D) = 0

Where, J_D = Ɛ₀ (ϐE/ϐt)

is the displacement current density, and has the same dimensions as the current density. Since J_D is caused by a changing electric field, it will be non-zero between the capacitor plates.

Using Eq. [Δ . (J + J_D) = 0], Ampere’s Law can then be modified to make Δ • (Δ x B) = 0, i.e.

Δ x B = μ₀ J + μ₀ Ɛ₀ (ϐE/ϐt)

which is Ampere’s law as modified by Maxwell. From this we may conclude that currents and displacement currents are on an equal footing in electrodynamics, and that a changing electric field induces a magnetic field.

Returning to the problem of the charging capacitor, and assuming the electric field is uniform between the plates and zero elsewhere, Gauss’ law gives

E = (σ / Ɛ₀) = (1/ Ɛ₀) (Q/A)

where a is the surface charge density, Q is the charge and A the plate area. Thus between the plates the displacement current is

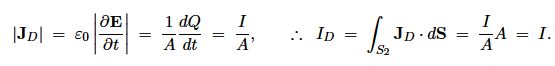
Hence, the total displacement current I_D between the plates is identical to the current I in the wires charging the plates.