An elastic spring is attached to the ceiling. A block with mass m is attached to the spring, and the spring is stretched by the distance l.
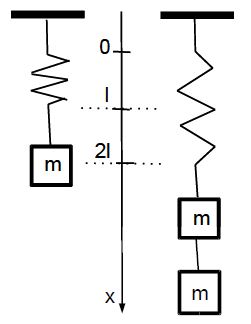
If two blocks with total mass 2m are attached, the spring is displaced by the distance 2l. The forces on the block are the weight mg [downward] and the Elastic Spring Forces [upwards]. Because the block is in mechanical equilibrium, the net force on the block is zero. We conclude that the elastic force is a linear restoring force,
Felast = – kx,
where k is the spring constant with unit [k] = [F]/[x] = N/m. We thus have F > 0 for x < 0 and F < 0 for x > 0.
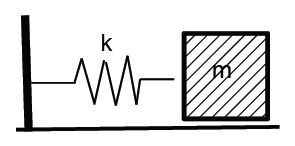
We consider a block with mass m sliding on a frictionless horizontal surface. The force along the horizontal direction is given by F = Felast = -kx so that the equation of motion of the block follows F = ma = – kx, or
a = – (k/m)x.
We know that, ω2 = k/m so that
T= 2π √(m/k)
Springs are stiffer for greater values of the spring constant. T= 2π √(m/k), then shows that stiffer springs oscillate with shorter periods.













