A polyene molecule is a linear hydrocarbon chain of alternating single and double bonded C-atoms. Polyene molecules are important in biological processes and below Figure shows such a short polyene molecule.
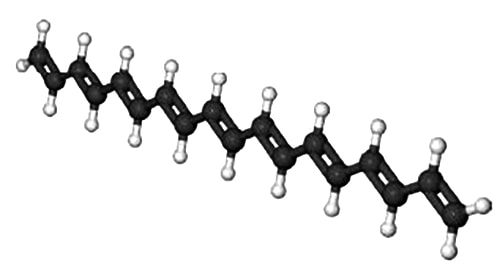
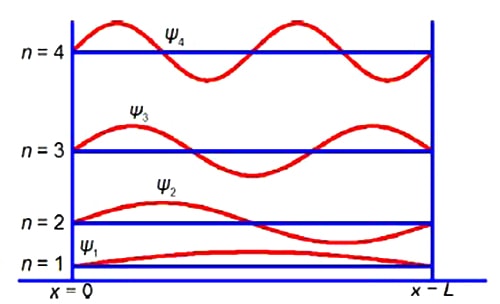
Because of the alternation of the single and double bonds, the n-electrons are mobile and may move along the length of the polyene. Thus we may treat the polyene molecule as a one-dimensional box of length L which confines the n-electrons. This interesting and important quantum mechanical concept will be discussed in your Chemistry degree. Below Figure shows some of the different wavefunctions for the allowed solutions for the mobile n-electrons as the quantum number n increases so does the energy of the n-electron in that level.
The total probability of finding a π-electron at a certain position x, measured from one end of the one-dimensional box of length L is given below.
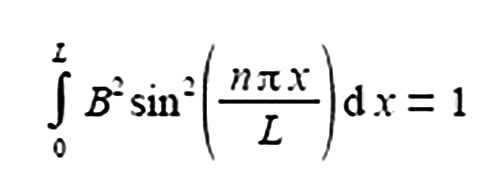
Where the sine is in radians not degrees hence the need for π; x is the distance along the molecule from one end; n is a constant called a quantum number which may take any of the values n = 1, 2, 3, and B is a constant to be evaluated. Use the standard integral below to integrate the probability equation from x = 0 to x = L and thus find B in terms of L the length of the molecule (C is the constant of integration).
ʃ sin2 (ax) dx = x/2 – [(sin 2ax) / 4a] + C
Now
Using the standard integral,
ʃ sin2 (ax) dx = x/2 – [(sin 2ax) / 4a] + C
Take the constant B2 outside the integral as B is not a function of x, let a = nria in the standard integral gives
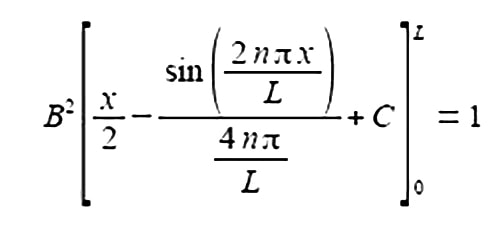
Substituting the limits x = L and x = 0 and the constant of integration cancels out.
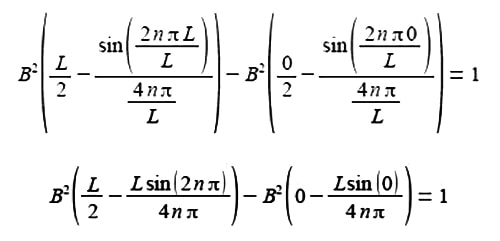
The term 2nπ is in radians not degrees and as n is an integer, sin(2nπ) = 0, prove this by using your calculator to find sin(π) in radians. The second term of the upper limit is zero and both terms of the lower limit are also zero.
B2 (L/2) = 1
B2 = 2/L
B = √ (2/L)
Although not directly part of the question, we now have the full equation for the wavefunctions of a π-electron in a given quantum level n of a polyene molecule as shown in above Figure.
Ψn = √ (2/L) sin (nπx / L)











