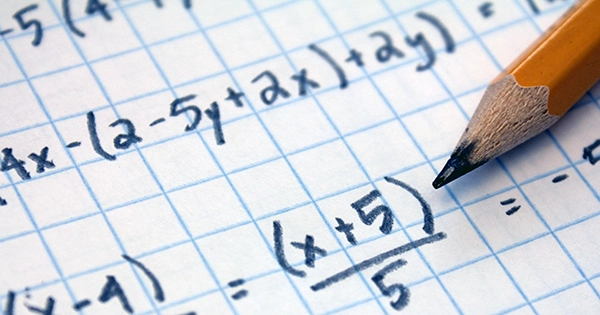Can you pick out the positive numbers whose reciprocals add to one if we offer you a collection of positive integers? Let’s use the numbers 2, 4, 6, 8, 10, and 12 as an example. We can discover that by removing 2, 4, 6, and 12 from the collection. It’s not a simple problem, but it doesn’t appear to be too difficult either, does it? However, some mathematicians believe that a variant of this subject “may be the oldest problem ever.” It now has an answer, due to a recent study by mathematician Thomas Bloom. To give it its proper name, the density variant of the Erds–Graham issue is as follows.
That’s essentially mathematician talk for the question we posed at the beginning, but with one key difference: the set we begin with is now infinitely huge. The wonderful thing about arithmetic is that it’s rather simple to find indefinitely huge objects. One example is the collection of all odd integers greater than two.
Because this set does not contain all positive integers, it is clearly a subset of the natural numbers — or, in math jargon, a subset of the natural numbers. It is, nevertheless, a set with a positive density. That’s a rather complicated mathematical concept, but think of it this way: no matter how high we count, we have a non-zero chance of landing on a number in set A – in other words, an odd number greater than one. Even if we’re talking billions, odd numbers exist, right?
So now that we’ve got our set A N with positive density, we need to figure out what to do with it. The goal, like previously, is to discover a group of integers inside the set that total to one when you take their reciprocal – that is, when you use them as the denominator in a fraction with numerator one. Beautiful! But it isn’t enough: in order to verify the statement, we must be able to discover those reciprocals in every set a may be picked – which is a considerably more difficult task.
“I just felt this was an impossible subject that no one in their right mind could ever ever solve,” said Andrew Granville, a mathematician at the University of Montreal. “I couldn’t find any clear tools to fight it.” Bloom discovered the answer practically by accident, given how complex the challenge was. It all started in September, when he was requested to give a talk about a similar – but weaker – result established by a mathematician named Ernie Croot twenty years before.
“I don’t think I was aware of this issue until I read Croot’s work!” IFLScience spoke with Bloom. “It’s safe to say he authored his article long before I became interested in mathematics.” The coloring variant of the Erds–Graham issue was what Croot had solved. It gets its name from the fact that it requires “coloring” subsets – imagine of it as sorting the members of the set A into a finite number of distinct colored bins.
Ronald Graham would later remark, “Erds and I enjoyed this issue so much that we offered a reward [of] $500 for its solution.” He said, “As it turned out, Erds did not survive to witness the answer.” “When I asked Ernie whether he wanted a check for the $500 signed by Erds, he indicated he would be happy to be paid in this manner. (For such eventualities, I maintained a number of pre-signed checks from Erds.) ”
The coloring variant of the Erds–Graham problem states that after the infinite set has been divided into these colored bins, we can absolutely discover one bin that includes integers whose reciprocals amount to one. Croot’s much-publicized proof was published in the Annals of Mathematics in 2003, after it had been unsolvable for over two decades. “Croot’s argument is a delight to read,” University of Georgia mathematician Giorgis Petridis told Quanta. “It necessitates a great deal of technical prowess, originality, and innovation.”
The coloring issue is similar to the density problem in that both require us to discover a subset of integers whose reciprocals total to one, but there is one key difference. The complete set A has been divided into bins in the coloring issue. You don’t know how it’s been divided, but that’s not important; all you need to prove is that there’s one bin with numbers that add up to the total. Croot devised a proof in his work to show that at least one bin will always include enough of these good numbers – numbers with low prime factors, or “smooth numbers” in mathematical parlance – to satisfy the theorem.