Kepler’s Law from Newton’s law
Kepler’s Laws are magnificent as an explanation of the motions of the planets. However, they present no clarification of why the planets travel in this system. Moreover, Kepler’s Third Law simply works for planets around the Sun and does not be appropriate to the Moon’s orbit around the Earth or the moons of Jupiter. Isaac Newton (1642-1727) provided a further universal clarification of the motions of the planets through the improvement of Newton’s Laws of Motion and Newton’s Universal Law of Gravitation.
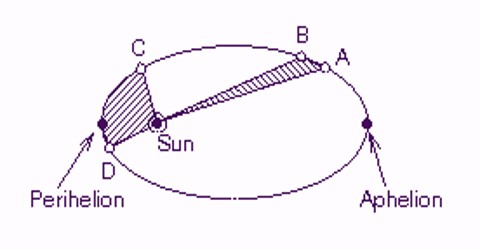
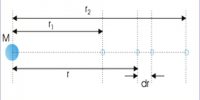
Suppose a planet is revolving, in a circular path of radius ‘r’ keeping the sun at the center at a speed ‘v’ (figure). If the mass of the sun is ‘M’, radius of the planet (earth) is ‘m’ and time period of the planet is T, then according to the gravitational law of Newton, the gravitational force between any two bodies is,
Fg = GMm/r2 … … … (1)
Here G = Gravitational constant
Again, centripetal force necessary for circular motion of the planet is,
FC = mv2/r … … … (2)
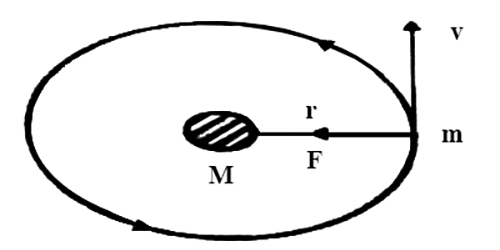
Force of the attraction of the earth on the planet gives this centripetal force.
So, Fg = FC
or, GMm/r2 = mv2/r
Or, GM/r = v2 … … … (3)
If T is the time period of the planet i.e., if T is the time taken to revolve once around the sun at an orbit of radius r, then linear velocity, v = 2πr/T
By inserting this value in equation (3) we get,
GM/r = (2πr/T)2
or, GM/r = (4π2r2)/T2
So, T2 = (4π2/GM) x r3
In this equation (4π2/GM) is Constant,
T2 = constant x r3
So, T2 ∞ r3
i.e., square of the time period of the planet is proportional to the cube of the distance between the sun and the planet in the orbit. It is Kepler’s third law.