X-ray diffraction is a standard method of chemical analysis to determine the structure of crystalline solids. The X-rays photons are scattered from the electrons in the atoms and interfere to give bright spots, i.e. the crystal planes of atoms act as diffraction gratings.
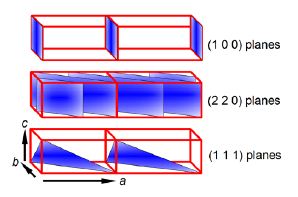
The crystal planes of atoms are described by Miller indices (h k 1) from the ratios of the plane’s coordinates (x, y, z) to the lengths of the axes of the unit cell a, b, c (which are not necessarily at right angles). We then take the reciprocal of these ratios; and if necessary multiply these reciprocals by the smallest number to converted them to integers. In below Fiure the crystal plane are shown in blue and these Miller indices become really useful for the planes that are parallel to the an axis. So for the top diagrams the first plane which is not at the origin is a la, and it is parallel to the b and c axes so these intercepts are both at la, ∞ b, ∞ c which gives the ratios and the plane’s Miller indices using the fact that 1/∞ = 0.

The intensity of the scattered beam of X-rays from the hkl plane of a crystal is proportional to F* F where F, the structure factor for a particular crystal is determined by the positions of the atoms in the various crystal planes and is its complex conjugate.
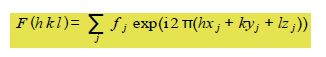
The summation runs over j the number of atoms in the unit cell, with each atom having a scattering factor fj and fractional coordinates (xj, yj, zj) within the unit cell.
Metallic sodium crystals have a body-centred cubic structure with two atoms per unit cell located at (0,0,0) and (1/2,1/2,1/2) respectively. Firstly, use the above equation to find F the structure factor for metallic sodium, and secondly, use Euler’s formula to determine its real and imaginary parts. Thirdly, show that X-ray diffractions “reflections” occur (i.e. F(hk1) 0) only if the quantity h+k+l is even, but not if it is odd.
Solution
Firstly, from the definition of the structure factor, we have to substitute the values for each atom in the unit cell.
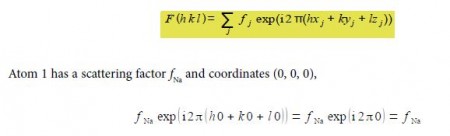
since exp(0) = 1 the first sodium atom’s contribution to the structure factor F summation is just fna.
Atom 2 has a scattering factor fna. and coordinates (1/2, 1/2, 1/0) and makes a contribution to the summation of,
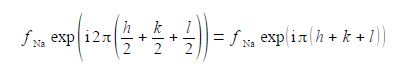
Adding the effects for the two atoms gives the structure factor F for metallic sodium’s body-centred unit cell,
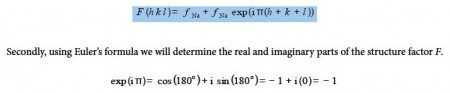
where we must use radians (π radians = 180°). For the particular example of a body-centred cubic structure the real part is -1 and the imaginary part is zero, but this will not necessarily happen for other crystal structures!
Thirdly, we have to investigate the behaviour of the function exp in(h + k + 1)) for different values of h+k+1. As h, k and I are all integer quantities their sum must also be an integer. Let’s call this sum N = h + k +I and we must now look at the behaviour of exp(iNπ) for various values of integer N. So we have when N = 1, 3, 5, …
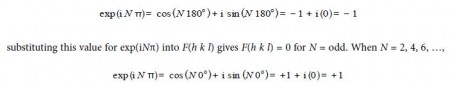
This means that the structure factor F is either of the two values given below dependent upon the Miller indices of the crystal plane,
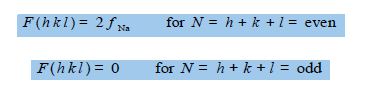
i.e. there is no X-ray scattering observed for h + k + I = odd crystal planes but only from h + k + I = even planes for the particular crystal structure of metallic sodium.