Electric field due to an infinite charged plane sheet (Application of Gauss’s Law):
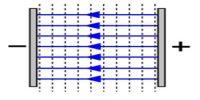
Consider an infinite plane sheet of charge with surface charge density σ. Let P be a point at a distance r from the sheet (Figure) and E be the electric field at P.
Consider a Gaussian surface in the form of the cylinder of cross− sectional area A and length 2r perpendicular to the sheet of charge.
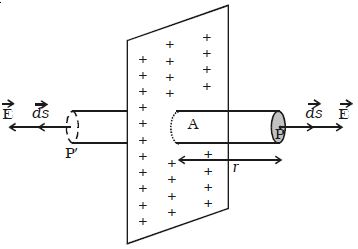
Fig: Infinite plane sheet
By symmetry, the electric field is at right angles to the end caps and away from the plane. Its magnitude is the same at P and at the other cap at P′.
Therefore, the total flux through the closed surface is given by
φ = [ϐ E.ds]p + [ϐ E.ds]p1
so, E A + E A = 2 E A
If σ is the charge per unit area in the plane sheet, then the net positive charge q within the Gaussian surface is, q = σA
Using Gauss’s law, 2 EA = σA/ε0
then, E = σ/2ε0