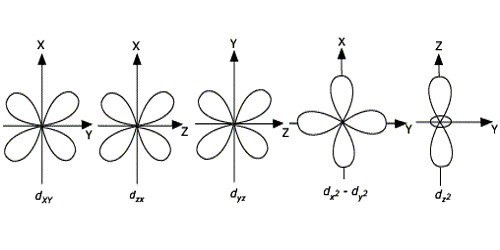
For d-orbitals or d-subshell, Ɩ = 2, there are five values of m namely -2, -1, 0, 1, 2. It means d- orbitals can have five orientations. They have an even more complex angular distribution than the p orbitals. These are represented by dxy, dyz, dzx, dx2-y2 and dz2; for example, 3dxy, 3dyz, 3dzx, 3dx2-y2 and 3dz2. The dxy, dyz, and dzx orbitals have the same shape i.e., cloverleaf shape but they lie in XY, YZ, and ZX planes respectively. Hence, we can say that there are five d-orbitals. These different orbitals essentially have different orientations. The dz2 orbital is symmetrical about Z-axis and has a dumbbell shape with a doughnut-shaped electron cloud in the centre. The dx2-y2 orbital is also clover leaf-shaped but its leaves are directed along the X and Y-axis.
The reason for the presence of four lobes in any d orbital lies in the fact that the d – orbitals have two nodes, and hence two changes in algebraic sign of ψ, which lead to four lobes. d orbitals have two angular nodes (two angles at which the probability of electron is always zero).
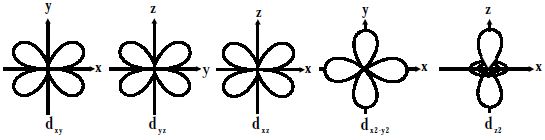
Fig: Shapes of d-orbitals
There is a set of five d orbitals (with complicated shapes and names) as well as the 3s and 3p orbitals (3px, 3py, 3pz). At the third level, there is a total of nine orbitals altogether. The magnetic orbital quantum number for d orbitals is given as (-2,-1,0, 1,2). Out of these five d orbitals, shapes of the first four d-orbitals are related to each other, which is different from the dz2 orbital whereas the energy of all five d orbitals is the same.