A certain amount of energy is needed to start a current in a circuit – work is done against the back emf to get the current going and set up the magnetic field. The work done to move unit charge against the back emf in one trip around the circuit is Ɛ. The amount of charge per unit time passing down the wire is I, so the work done per unit time is
(dW/dt) = – Ɛ I = LI (dI/dt)
The total work done in establishing the magnetic fields are
W = L ʃ IDI = ½ LI2
We can show that the work W done in establishing the magnetic fields are stored as magnetic field energy U. In establishing the field, the power source does work at rate (dW/dt) ≈ dU /dt = -I Ɛ = – ʃ J.E, for current density J(r) = Δ x H (r) and induced electric field E(r) = – ϐ A / ϐt.
Then
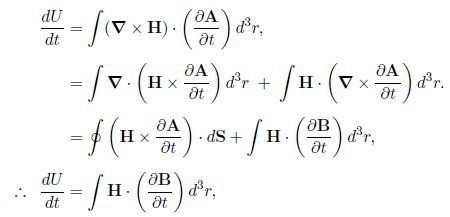
As the volume integrals are over all space, the surface integral is for the surface at r = ∞, and with the integrand dropping faster than dS ≈ r-2. This tells us that the change in the magnetic energy density due to a small change dB(r) in the magnetic field is
d[u(r)] = H (r) • dB (r)
For linear materials;
d[u(r)] = H (r) . d[μ H (r) = ½ d [H (r). μ H (r)]
= ½ d [H (r) . B (r)]
Hence, the magnetic energy density in linear materials is
![]()