Experiment: Determination of Specific heat of liquids by Newton’s law of cooling
Theory: The amount of heat, needed to increase the temperature of unit mass of a material by 1°C is called the specific heat of that material. It is denoted by S.
In the same environment, rate of change of cooling of an object is directly proportional to the difference of temperature between the object and the surrounding. This is the theory of cooling method. Difference of temperature of the object and the surrounding must be small. When a liquid is heated of higher temperature and placed to cool. Then the rate of heat lost by a temperature of the liquid is directly proportional to the difference in temperature of the surrounding.
Suppose, water equivalent of the calorimeter along with the stirrer = W kg
Mass of the experimental liquid in the calorimeter = M kg
Specific heat of the liquid = S J kg-1K-1
Time taken to cool the liquid from temperature- θ10 to θ20 = t1 sec
Mass of water having volume equal to that of the liquid = m1 kg
Specific heat of water = S1 J kg-1 K-1
Time taken to cool water from temperatures, θ10 to θ20 = t2 sec
So, rate of cooling of the liquid = [(MS + W) (θ1 – θ2)] / t1 Js-1
and rate of cooling of water = [(M1S1 + W) (θ1 – θ2)] / t2 Js-1
According Newton’s law of cooling, rate of cooling in these two cases is equal.
so, [(MS + W) (θ1 – θ2)] / t1 Js-1 = [(M1S1 + W) (θ1 – θ2)] / t2 Js-1
or, [(MS + W) (θ1 – θ2)] / t1 = [(M1S1 + W) (θ1 – θ2)] / t2
or, S = 1/M [{(m1S1 + W)t1 /t2} – W]
or, S = 1/M [t1/t2 (m1S1 + W) – W] J kg-1 K-1… … … (1)
Now putting the values of M, m1, S1, W, t1 and t2 in equation (1) we can find the value of S.
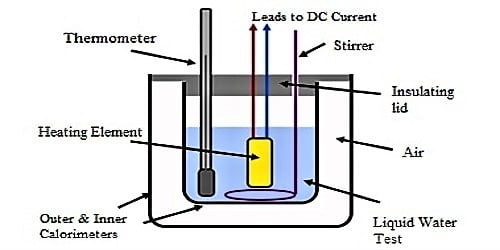
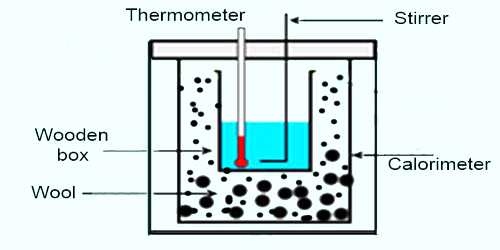
Apparatus: (1) a calorimeter with a stirrer, (2) a chamber having two walls, (3) a sensitive thermometer, (4) balance, (5) burner, (6) stop-watch etc.
Procedure:
(1) Weight is taken of a clean and dry calorimeter along with its stirrer.
(2) Then water is heated in another container between temperature of 70°C to 75°C and that water is poured in the calorimeter upto a fixed mark. This calorimeter is placed in a two-walled chamber.
(3) Water is stirred slowly and slowly by a stirrer and temperature of water is recorded in 1°C interval. As the temperature of water is more than room temperature, so temperature of water gradually decreases. In this way 20 to 25 readings of temperature are recorded and then weight of the calorimeter along with water is taken. From the difference of subtraction of these two readings weight of water is found out.
(4) Now water is thrown away from the calorimeter and it is cleaned and dried. Then experimental heated liquid from 70°C to 75°C is poured in the calorimeter upto the previous mark. The calorimeter along with the liquid is placed inside chamber.
(5) Then the liquid is stirred slowly and following procedure (3) temperature is recorded in each degree interval of temperature. In this way 20-25 readings are taken. Afterwards calorimeter with liquid is taken. From the difference of weights of 3rd and the first one weight of the liquid is found out.
Observation and Manipulation:
Table: Mass of water and liquid

Specific heat of the material of the calorimeter = Sꞌ J kg-1 K-1
So, Water equivalent, W = W1 x S1 Kg
Calculation: S = 1/M [t1/t2 (m1S1 + W) – W] J kg-1 K-1
Result: Specific heat of the given liquid, S = … … J kg-1 K-1
Precautions:
(1) Calorimeter should be clean and dry.
(2) Weight should be accurate.
(3) Temperature should be measured accurately.
(4) Measurement of time should be accurate.
Discussions: (1) If the calorimeter is not clean and dry, it weight is not accurate and readings of temperature and time are not accurate, then experimental accurate.
(2) If equal volumes of water and liquid are not taken then error will appear in the result.
(3) Bottom of the calorimeter is to be made black. As a result heat radiation capacity increases.
(4) No volatile liquid is to be taken.