Let consider a particle of mass moving along the circular path of radius r as shown in Figure. Let the initial position of the particle be A. P and Q are the positions of the particle at any instants of time t and t + dt respectively.
Suppose the particle traverses a distance ds along the circular path in time interval dt. During this interval, it moves through an angle dθ = θ2 – θ1. The angle swept by the radius vector at a given time is called the angular displacement of the particle.
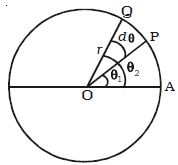
Fig: Angular Displacement
If r be the radius of the circle, then the angular displacement is given by dθ = ds/r. The angular displacement is measured in terms of radian.