Explain Angular Momentum of a Rigid Body

Let consider a system of n particles of masses m₁, m₂ … …m_n situated at distances r₁, r₂ … …r₃ respectively from the axis of rotation (Figure).

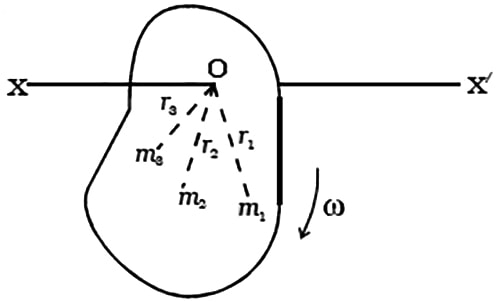
Let v₁, v₂, v₃ … … be the linear velocities of the particles respectively, then the linear momentum of first particle = m₁ v₁.

Since v₁ = r₁ ω; the linear momentum of first particle = m₁ (r₁ ω)

The moment of linear momentum of first particle = linear momentum x perpendicular distance

= (m₁ r₁ ω) x r₁

angular momentum of first particle = m₁ r₁² ω

Similarly,

Angular momentum of second particle = m₂ r₂² ω

Angular momentum of third particle = m₃ r₃³ ω and so on.

The sum of the moment of the linear momentum of all the particles of a rotating rigid body taken together about the axis of rotation is known as the angular momentum of the rigid body.