Laws of Reflection in the Light – Huygens’s Principle
Each point on any wavefront is considered as the source of oscillation or disturbance. The waves generated from those secondary sources progress forward with the same velocity of the principal wave. It a surface is drawn by the tangents of those secondary waves at any time, then that surface will represent the new position of the wavefront at that time.
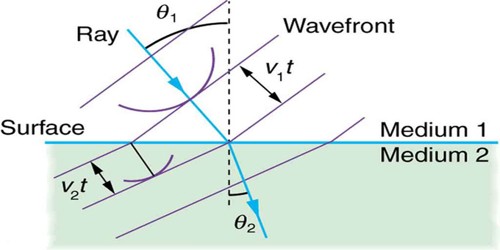
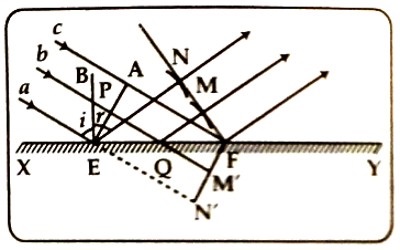
Let XY be a plane reflecting surface and a, b, c are three parallel rays of light. These rays are incident obliquely on the surface XY [Figure]. Suppose EPA is the wavefront of these parallel rays. Each of its points will act as the center of disturbance and will create tiny secondary waves. These secondary waves will spread all over the surface. Let a ray of the light front the point A is incident at point F of the XY surface at time t. In the meantime, disturbance of E will reach point N and the disturbance of Q will reach point M. So, the reflected wavefront FMN will be obtained. If the velocity of light in air is ‘v’, then FA = vt. Now, taking E as center and FA = vt as the radius, an arc drawn then FMN will be found out. By drawing the tangent of FMN, the new wavefront will be obtained. This is the reflecting wavefront.
Proof of the laws of reflection:
In the triangles ΔAEF and ΔNEF, ∠ EAF = ∠ ENF = 1 right angle, AF = EN = vt and EF is common to both.
The triangle are congruent and ∠ AEF = ∠ EFN … … (1)
Now if EB is the normal at the point of incidence E, then
∠ aEB + ∠ BEA = ∠ BEA + ∠ AEF = 1 right angle i.e.. 900
So, ∠ aEB = ∠ AEF = angle of incidence, ∠ i … … … (2)
Again, ∠ NEB + ∠ NEF = ∠ EFN + ∠ NEF = 1 right angle
So, ∠ NEB = ∠ EFN = angle of reflection, ∠ r… … … (3)
From the equation (1), (2), and (3), it can be written, angle of incidence ∠ i = angle of reflection, ∠ r. By it the second law of reflection of light is proved.
Again, the incident ray aE, the reflected ray EN, and the normal EB drawn at the point of incidence are at the same surface. So, by it, the first law of reflection of light is proved.
The two laws of reflection are proved on the basis of the wave theory of light.