Multiplying the polar form of the complex number:
z =|z| (cos Ө + i sin Ө)
by itself n times then we multiply the size |z| by itself n times, giving the final size |z|n. We add the angle Ө to Ө, n times, giving the final angle nӨ. The resultant polar form is called de Moivre’s formula (also known as de Moivre’s theorem),
zn =|z|n (cos Ө + i sin Ө)
where n may be positive, negative, integer, or fractional, although if n is fractional then the result is multi-valued. I will give the two most common examples of the use of de Moivre’s theorem, the square root and the cube roots of of a complex number,

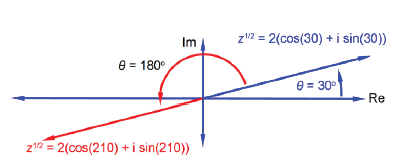
There are two square roots of a complex number separated by 180°, i.e. 360°/2, as in Fig. 3.10. All you need to do is find the first root (the principal root) and then add another root at 180° to the first square root.
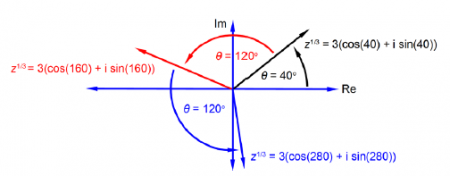
The second Example of the n being fractional is the cube root of :
z = 27 (cos 1200 + i sin 1200)
As z is identical for 120° and 120° plus either one or two revolutions i.e. (120° + 360° = 480°) and (120° + 360° + 360° = 840°) we have,
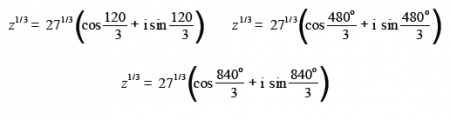
![]()
There are three cube roots of a complex number each separated by 120°, i.e. 360°/3, as in below Figure. All you need to do is find the first root and then add 120° twice for the other two cube roots.