Gauss’s Law to determine Electric Field near a Charged Plane Conductor

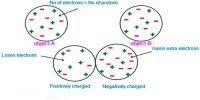
Electric field near a charged plane conductor:

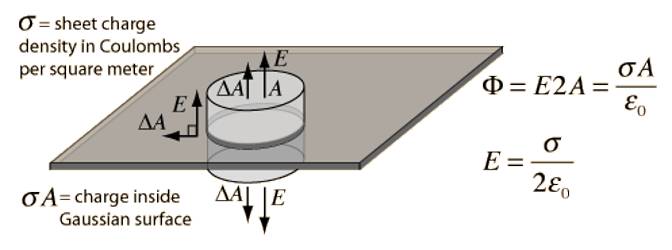
For an infinite sheet of charge, the electric field will be perpendicular to the surface. Therefore only the ends of a cylindrical Gaussian surface will contribute to the electric flux. Suppose AB is the surface of a charged plane. Its charge density is σ. The electric field is to be determined for this charge. In this case, a cylindrical Gaussian surface perpendicular to the charge sheet is used. The resulting field is half that of a conductor at equilibrium with this surface charge density.

On both sides of the plane surface, two points C and D are considered and let us consider a cylinder of cross-sectional area ‘da’ through these two points [Figure]. Now the normal induction on the surface ‘da’ will be ‘Eda’ and it is outward. Similarly, at point D the normal D induction is ‘Eda’ on the surface da and its direction is outward. Again normal induction on the curved surface of the cylinder is ∫Eda^→. So, total normal induction on the hypothetical cylinder = Eda + Eda = 2Eda and its direction is outward.

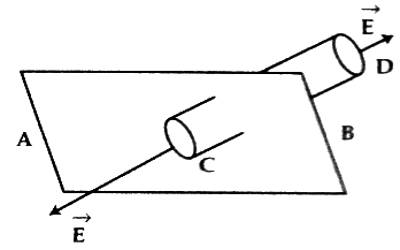
According to Gauss’s Law total normal induction = σda / ε₀

So, 2Eda = σda / ε₀

or, E = σ / 2ε₀ …. …. (1)

In vector form, we can write,

E^→ = (σ / 2ε₀) ň

Here, ň is outward perpendicular unit vector on the given plane surface. It is seen from the equation (1) that the electric field due to the charged plane is independent of distance.