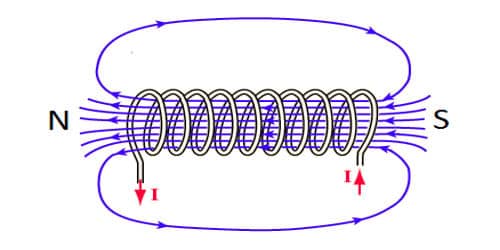
A long closely wound helical coil is called a solenoid. The animation shows a section of the stretched out solenoid. The direction of the magnetic field due to circular closed loops (solenoid) is given by right-hand palm-rule. The magnetic field due to the solenoid is the vector sum of the magnetic fields due to current through individual turns of the solenoid. When a current-carrying solenoid is freely suspended, it comes to rest like a suspended bar magnet pointing along north-south. The magnetic fields associated with every single turn are almost concentric circles and hence tend to cancel between the turns. The magnetic polarity of the current-carrying solenoid is given by the End rule.
Experiment: Magnetic induction due to a long solenoid carrying current
Let consider an infinitely long solenoid having n turns per unit length carrying a current of I. For such an ideal solenoid (whose length is very large compared to its radius), the magnetic field at points outside the solenoid is zero.
A long solenoid appears like a long cylindrical metal sheet (Figure). The upper view of dots is like a uniform current sheet coming out of the plane of the paper. The lower row of crosses is like a uniform current sheet going into the plane of the paper.
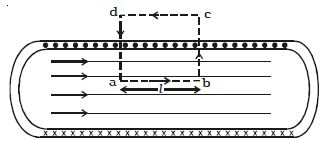
Fig: Magnetic field due to a long solenoid
To find the magnetic induction (B) at a point inside the solenoid, let us consider a rectangular Amperean loop abcd. The line integral ∫ B.dl for the loop abcd is the sum of four integrals.
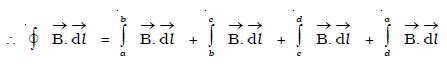
If l is the length of the loop, the first integral on the right side is Bl. The second and fourth integrals are equal to zero because B is at right angles for every element dl along the path. The third integral is zero since the magnetic field at points outside the solenoid is zero.
∴ ∫ B.dl = Bl … (1)
Since the path of integration includes nl turns, the net current enclosed by the closed-loop is
I0 = Inl … (2)
Ampere’s circuital law for a closed-loop is
∫ B.dl = μ0I0 … (3)
Substituting equations (1) and (2) in equation (3)
Bl = μ0 Inl
∴ B = μ0 nI … (4)
The solenoid is commonly used to obtain a uniform magnetic field.
By inserting a soft iron core inside the solenoid, a large magnetic field is produced
B = μnI = μ0 μ1 nI … (5)
when a current-carrying solenoid is freely suspended, it comes to rest like a suspended bar magnet pointing along north-south.