In the field of quantum computing and quantum machine learning, scientists have developed a technique known as “Time-dependent Stochastic Parameter Shift.” This ground-breaking method transforms the estimation of gradients or derivatives of functions, which is a critical step in many computational tasks.
Quantum computing employs quantum mechanics to process and store information in a manner distinct from traditional computers. While traditional computers rely on bits that can be either 0 or 1, quantum computers use quantum bits (qubits). Qubits are unique in that they can be both 0 and 1 at the same time, a state known as superposition. Because of this unique property, quantum computers can solve specific problems much faster than classical computers.
Le Bin Ho of Tohoku University’s Frontier Institute for Interdisciplinary Sciences developed a technique called “Time-dependent Stochastic Parameter Shift” in the realms of quantum computing and quantum machine learning, which was recently published in EPJ Quantum Technology. This ground-breaking method transforms the estimation of gradients or derivatives of functions, which is a critical step in many computational tasks.
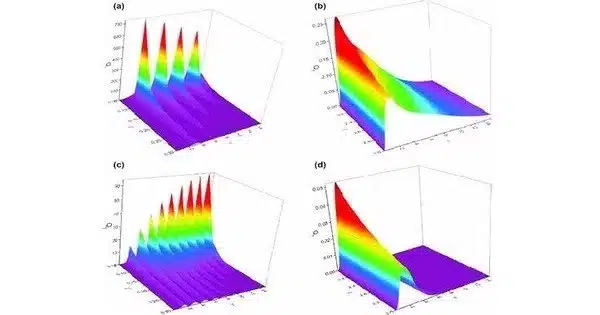
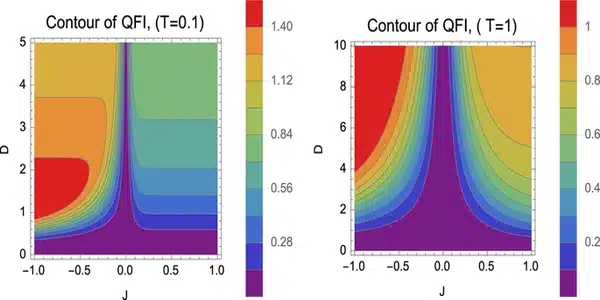
Our time-dependent stochastic method is applicable to the broader applications for higher-order derivatives and can be employed to compute the quantum Fisher information matrix (QFIM), a pivotal concept in quantum information theory and quantum metrology.
Le Bin Ho
Derivatives are typically computed by dissecting the function and calculating the rate of change over a small interval. However, even traditional computers cannot divide indefinitely. Quantum computers, on the other hand, can complete this task without having to discretize the function. This feature is possible because quantum computers operate in a realm known as “quantum space,” which is characterized by periodicity and the absence of the need for infinite subdivisions.
Comparing the sizes of two elementary schools on a map is one way to demonstrate this concept. To accomplish this, one could print out school maps and then cut them into smaller pieces. After cutting, arrange these pieces in a line and compare their total length. However, the pieces may not form a perfect rectangle, resulting in errors. To minimize these errors, an infinite subdivision would be required, which would be impractical even for classical computers.
A more straightforward method involves weighing the paper pieces representing the two schools and comparing their weights. This method yields accurate results when the paper sizes are large enough to detect the mass difference. This bears resemblance to the parameter shift concept, though operating in different spaces that do not necessitate infinite intervals.
“Our time-dependent stochastic method is applicable to the broader applications for higher-order derivatives and can be employed to compute the quantum Fisher information matrix (QFIM), a pivotal concept in quantum information theory and quantum metrology,” according to Le.
“QFIM is inextricably linked to a variety of disciplines, including quantum metrology, phase transitions, entanglement witness, Fubini-Study metric, and quantum speed limits, making it a fundamental quantity with numerous applications.” As a result, calculating QFIM on quantum computers may pave the way for quantum computers to be used in fields as diverse as cryptography, optimization, drug discovery, materials science, and beyond.”
Le also demonstrated how this method can be used in a variety of applications, such as quantum metrology with single and multiple magnetic fields, as well as Hamiltonian tomography applied to complex many-body systems. He also meticulously compared the new method to the exact theoretical method as well as another approximation model known as the Suzuki-Trotter. Despite being close to the theoretical approach, the Suzuki-Trotter approximation deviated from the true value. To improve the results of the Suzuki-Trotter approximation, an infinite subdivision of the Suzuki-Trotter steps would be required.