Law of Refraction according to Fermat’s Principle
The law of refraction of light, Fermat’s principle or Snell’s Law states that the ratio of the sines of the angles of incidence and refraction is equal to the inverse ratio of the indices of refraction of the two media. Fermat’s principle states that “light travels between two points along the path that requires the least time, as compared to other nearby paths.” From Fermat’s principle, one can derive the law of refraction.
Law of Refraction
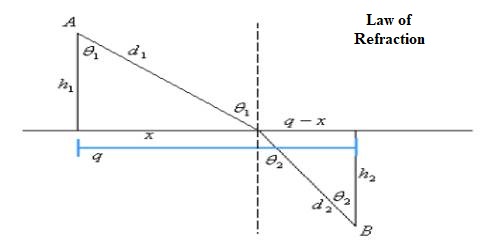
Let light ray PQ, starting from point P and traveling through Q reaches to a stationary point R. Light ray PQ being incident on MM’, the plane of separation between the media a and b, at an angle ‘i’ and is refracted in the medium at an angle ‘r’ [Figure].
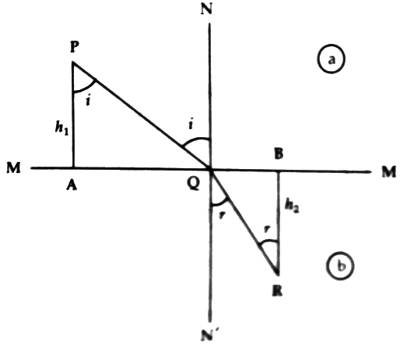
Normals PA and PB are drawn the separating plane MM’.
Suppose, PA = h1, RB = h2, AB = d and AQ = x. Then QB = d – x. If the velocities of light in the media a and b are respectively ca and cb and time taken by light to travel the paths PQ and QR is t, then
t = PQ/ ca + QR/ cb = √(h12 + x2)/ ca + √{(h22 + (d-x)2}/ cb
According to Fermat’s principle, time t will be the last time, so,
dt / dx = 0
so, dt / dx = {2x / [ca √(h12 + x2)]} – [2(d-x) / [cb√{(h22 + (d-x)2}]
or, 2 {x / [ca √(h12 + x2)]} – [(d-x) / [cb√{(h22 + (d-x)2}] = 0
or, {x / [ca √(h12 + x2)]} – [(d-x) / [cb√{(h22 + (d-x)2}] = 0
or, sin i / ca = sin r / cb
So, sin i / sin r = ca/cb = aμb
This is the second law of refraction or Snell’s law.
Again, the lines PQ and QR form a plane after meeting at point Q. Since PQR is the least path, so the separating plane NN’ between the two media will be normal on this plane. Since the normal NN’ is perpendicular to the separating plane, the plane in which PQ and QR are situated NN’ will also remain in the same plane. So, incident ray PQ, refracted ray QR and normal NN’ are situated in the same plane.
This is the first law of refraction.