A simple pendulum consists of the massless and inelastic thread whose one end is fixed to a rigid support and a small bob of mass m is suspended from the other end of the thread. Let l be the length of the pendulum. When the bob is slightly displaced and released, it oscillates about its equilibrium position. The figure shows the displaced position of the pendulum.
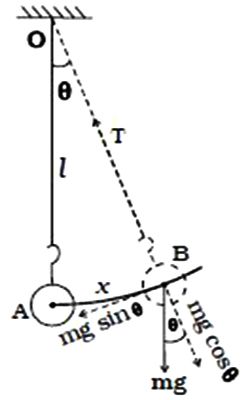
Suppose the thread makes an angle 6 with the vertical. The distance of the bob from the equilibrium position A is AB. At B, the weight mg acts vertically downwards. This force is resolved into two components.
(i) The component mg Cos θ is balanced by the tension in the thread acting along the length towards the fixed point O.
(ii) mg sin θ which is unbalanced acts perpendicular to the length of thread. This force tends to restore the bob to the mean position. If the amplitude of oscillation is small, then the path of the bob is a straight line.
F = – mg sin θ
If the angular displacement is small sin θ ≈ θ
F = – mg θ
But θ = x/l
So, F = – mg x/l











