Sound travels in air as a longitudinal wave. The wave motion is, therefore, accompanied by compressions and rarefaction and At compressions, the temperature of the air rises and at rarefactions, due to expansion, the temperature decreases. The above discrepancy observed was explained by Laplace in 1816. Laplace assumed that the propagation of sound in air is an adiabatic process not the isothermal.
Air is a very poor conductor of heat. Hence at a compression, air cannot lose heat due to radiation and conduction. At a rarefaction, it cannot gain heat, during the small interval of time. As a result, the temperature throughout the medium does not remain constant.
Laplace suggested that sound waves travel in the air under the adiabatic conditions and not under isothermal conditions.
For an adiabatic change, the relation between pressure and volume is given by
P Vγ = constant
Where γ = (CP/CV) is the ratio of two specific heat capacities of the gas.
Differentiating,
Pγ = -dP/(dV/V) = k
So, Pγ = k (Volume elasticity)
Therefore under adiabatic condition
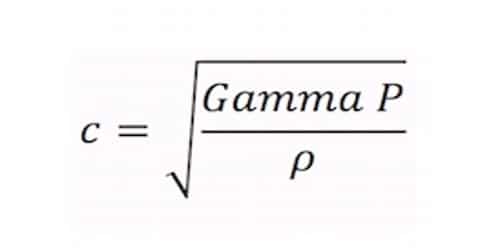
velocity of sound, v = √(k/ρ) = √(Pγ/ρ)
This is Laplace’s corrected formula.
Newton unspecified that the pressure-volume changes that happen when a sound wave travels through the gas are isothermal. According to Laplace, propagation of the sound waves in air or gas is not in the isothermal process as Newton assumed but it is an adiabatic process. Laplace was afterward able to obtain agreement between theory and experiment by assuming that pressure-volume changes are adiabatic.
Newton’s Formula & Laplace’s correction
Newton assumed that when sound propagates through air, the temperature remains constant (i.e. the process is isothermal).
So, the bulk modulus of elasticity B = BT = p
(isothermal bulk modulus BT of a gas is equal to its pressure).
Therefore at NTP,
p = 1.01 × 105 N/m2 and ρ = 1.3 kg/m3
Vair = √[(1.01 * 106)/1.3]
= 279 m/s
The experimental value of v in the air is 332 m/s at NTP. This discrepancy was removed by Laplace. This is a good agreement with the experimental value. Hence Laplace was able to correct Newton’s formula for the velocity of sound in air by considering the propagation of sound in air gas an adiabatic process rather than isothermal.