Power is a change in energy with respect to time. One way to add energy to a system is to apply force in the direction of displacement. This means power manifests as an (applied force changing over time) (in the direction of displacement) plus (an applied force) (in the direction of a displacement changing with respect to time). The second part of this second term is clearly a velocity. With a constant force (so the first term goes to 0), we’re left with power equals force times velocity.
Force is defined as the interaction between two bodies, or it can also be defined as the push or pull experienced by an object when an external force acts on it. Force is expressed in terms of Newton.
This is the concept that is explained in Newton’s first law of motion.
Newton’s First Law: Consider an object with no force acting on it. If it is at rest, It will remain at rest; if it is moving, it will continue its motion in a straight line at a constant speed. The force exists through contact or non-contact way.
Examples of contact forces are pushing a box and kicking a ball while examples of non-contact force are gravitational force and electrostatic force.
Force = (Mass) (Acceleration)
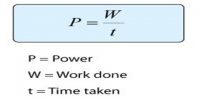
Power is defined as the amount of energy consumed when work is done in unit time. Power can also be defined as the rate at which work is done.
Power = Work done/Time taken
Watt is the unit of power.
Example: A lift motor has to move a fully laden lift 4m between floors in 1.5s. The lift has a mass of 1850 kg (ignore friction).
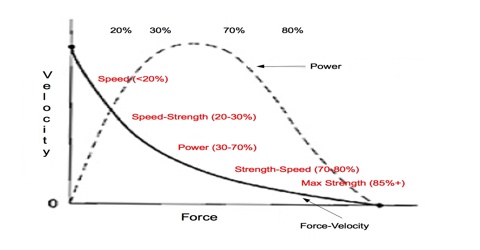
The relation between Power, Force, and Velocity
Suppose force F is acting on a body for time t. If during this time the body moves along the direction of the applied force to a distance s, then work done by that force is, W = F x s
Again, power, P = W/t= = Fs/t = Fv … … … (1) [as we know, s = v/t]
So, power = applied force x velocity of the body
If the displacement of the body, instead of being along with the force, is along a direction making an angle θ with the applied force, then
P = Fv cos θ
This equation represents a scalar product of two vector quantities.
According to vector notation, P = F.v. … … … (2)
This equation gives the relation between power, force, and velocity.
Power, in case of rotational motion:
In the case of rotational motion, we know,
Work = torque x angular displacement
Power, P = W/t = (Torque x angular displacement) / time
So, Power, P = Torque x angular velocity.