Example: A Yo-Yo is a uniform disk with mass m = 0.24 kg, outer radius R = 0.12 m, and inner radius r = 0.08 m. A string is wrapped around the inner ring. The string hangs from the ceiling and the Yo-Yo falls under the influence of it own weight.
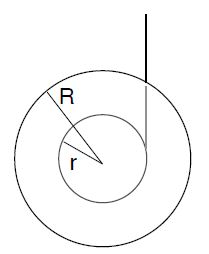
a) The Yo-Yo starts to fall from rest. After the Yo-Yo falls from the height h = 0.20 m, it travels with the speed v = 0.6 m/s. Find the angular velocity and acceleration at that instant rotational dynamics:
b) Find the moment of inertia of the Yo-Yo.
c) Find the tension in the string.
Solution: We have for the angular speed,
ω = v/r = 0.6m/s / 0.08m = 7.5 rad/s
We have the angular displacement Δθ = h/r = 0.20 m/0.08 m = 2.5 rad. Since ω0 = 0, the angular acceleration is

The gravitational energy is transformed into kinetic energy for translation and rotation. The translational kinetic energy is
KEtrans = ½ 0.24 kg (0.6 m/s)2 = 0.04 J.
Thus, the rotational kinetic energy is
KErot = PE— KEtrans = 0.47J – 0.04J = 0.43J= ½ I • ω2,
and
I = (2 • KErot / ω2) = 2 • 0.43J / (7.5 rad/s)2 = 1.53 x 10-2 kg • m2.
We have the torque exerted on the Yo-Yo,
τ = Iα = 1.53 x 10-2 kg m2 • 11.25 rad/s2 = 0.17 N m
For the tension T,
τ = Tr → T = τ/r = 0.17Nm / 0.08 m = 2.2 N.